Ford–Fulkerson method
The Ford–Fulkerson method is a technique for solving the maximum flow problem. The input is a flow network, 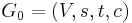 . Then the algorithm proceeds as follows:
. Then the algorithm proceeds as follows:
- Start with the empty flow,
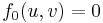 for all
for all 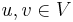 . The corresponding residual network is then equivalent to the original flow network,
. The corresponding residual network is then equivalent to the original flow network, 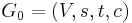 .
. - Find an augmenting path. Let
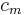 be the minimum residual capacity along the augmenting path. Push
be the minimum residual capacity along the augmenting path. Push 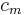 units of flow along the path, adding to the flow
units of flow along the path, adding to the flow 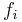 to give an augmented flow
to give an augmented flow 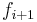 . Corresponding to the augmented flow is a new residual network,
. Corresponding to the augmented flow is a new residual network, 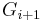 .
. - Repeat step 2 with the new flow and new residual network until an augmenting path can no longer be found. The final flow
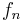 is a max flow.
is a max flow.
Correctness
If the algorithm terminates, then no augmenting path remains. By the augmenting path theorem, the flow 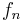 obtained is maximal.
obtained is maximal.
If the capacities are finite and integral, then the algorithm is guaranteed to terminate. It is not hard to see that an invariant of the algorithm is that the residual capacities are all integral after each augmenting step. Therefore 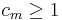 in each step, and the flow so far increases by at least one unit in each step. The algorithm must then terminate after no more than
in each step, and the flow so far increases by at least one unit in each step. The algorithm must then terminate after no more than 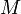 steps, where
steps, where 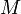 is the value of the max flow. A similar argument applies when all edge weights are rational.
is the value of the max flow. A similar argument applies when all edge weights are rational.
On the other hand, the algorithm is not guaranteed to terminate when the edge weights are allowed to be irrational.
Complexity
In step 2, we have a choice in how to find the augmenting path. The overall running time of the algorithm depends on the heuristic used to choose the path. In the most common choice of heuristic, known as the Edmonds–Karp algorithm, we always choose the shortest augmenting path using breadth-first search. (Note that the capacities are not lengths; each edge has length 1!) It is easy to see that the running time of such an approach is 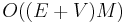 . Under a more sophisticated analysis, we can derive the bound
. Under a more sophisticated analysis, we can derive the bound 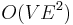 , which is independent of the edge capacities.
, which is independent of the edge capacities.
Other heuristics are possible. We could for example use depth-first search to find an augmenting path, which also gives an 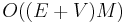 algorithm. Another possibility is to use a modification of Dijkstra's algorithm to find an augmenting path of maximal value, i.e., that maximizes
algorithm. Another possibility is to use a modification of Dijkstra's algorithm to find an augmenting path of maximal value, i.e., that maximizes 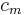 . In this case we have the bound
. In this case we have the bound 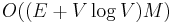 .
.
A more sophisticated approach, known as Dinic's algorithm, runs in 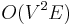 time, which can be sped up to
time, which can be sped up to 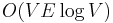 using link/cut trees.
using link/cut trees.