Depth-first search
Depth-first search (DFS) is one of the most-basic and well-known types of algorithm in graph theory. The basic idea of DFS is deceptively simple, but it can be extended to yield asymptotically optimal solutions to many important problems in graph theory. It is a type of graph search (what it means to search a graph is explained in that article).
Contents
Principles
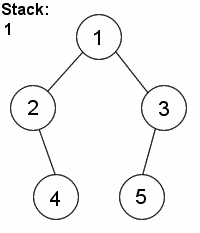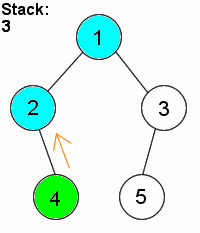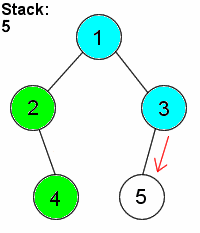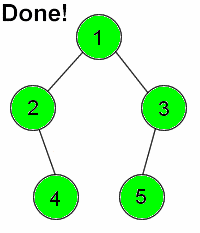
DFS is distinguished from other graph search techniques in that, after visiting a vertex and adding its neighbours to the fringe, the next vertex to be visited is always the newest vertex on the fringe, so that as long as the visited vertex has unvisited neighbours, each neighbour is itself visited immediately. For example, suppose a graph consists of the vertices {1,2,3,4,5} and the edges {(1,2),(1,3),(2,4),(3,5)}. If we start by visiting 1, then we add vertices 2 and 3 to the fringe. Suppose that we visit 2 next. (2 and 3 could have been added in any order, so it doesn't really matter.) Then, 4 is placed on the fringe, which now consists of 3 and 4. Since 4 was necessarily added after 3, we visit 4 next. Finding that it has no neighbours, we visit 3, and finally 5. It is called depth-first search because it goes as far down a path (deep) as possible before visiting other vertices.
Stack-based implementation
The basic template given at Graph search can be easily adapted for DFS:
input G
for all u ∈ V(G)
let visited[u] = false
for each u ∈ V(G)
if visited[u] = false
let S be empty
push(S,u)
while not empty(S)
v = pop(S)
if visited[v] = false
visit v
visited[v] = true
for each w ∈ V(G) such that (v,w) ∈ E(G) and visited[w] = false
push(S,w)
F has been replaced by a stack, S, because a stack satisfies exactly the necessary property for DFS: the most recently added item is the first to be removed.
Recursive implementation
There is a much cleaner implementation of DFS using recursion. Notice that no matter which vertex we happen to be examining, we execute the same code. That suggests that we might be able to wrap this code in a recursive function, in which the argument is the vertex to be visited next. Also, after a particular vertex is visited, we know that we want to immediately visit any of its unvisited neighbours. We can do so by recursing on that vertex:
function DFS(u)
if not visited[u]
visit u
visited[u] = true
for each v ∈ V(G) such that (u,v) ∈ E(G)
DFS(v)
input G
for each u ∈ V(G)
let visited[u]=false
for each u ∈ V(G)
DFS(u)
Note that we do not need to check if a vertex has been visited before recursing on it, because it is checked immediately after recursing. The recursive implementation will be preferred and assumed whenever DFS is discussed on this wiki.
Performance characteristics
Time
Most DFS algorithms feature a constant time "visit" operation. Suppose, for the sake of simplicity, that the entire graph consists of one connected component. Each vertex will be visited exactly once, with each visit being a constant-time operation, so 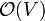 time is spent visiting vertices. Whenever a vertex is visited, every edge radiating from that vertex is considered, with constant time spent on each edge. It follows that every edge in the graph will be considered exactly twice -- once for each vertex upon which it is incident. Thus, the time spent considering edges is again a constant factor times the number of edges,
time is spent visiting vertices. Whenever a vertex is visited, every edge radiating from that vertex is considered, with constant time spent on each edge. It follows that every edge in the graph will be considered exactly twice -- once for each vertex upon which it is incident. Thus, the time spent considering edges is again a constant factor times the number of edges, 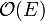 . This makes DFS
. This makes DFS 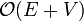 overall, linear time, which, like BFS, is asymptotically optimal for a graph search.
overall, linear time, which, like BFS, is asymptotically optimal for a graph search.
Space
Recursive implementation
For every additional level of recursive depth, a constant amount of memory is required. Notice that on the recursive stack, no vertex may be repeated (except the one at the top, in the current instance, just before the if not visited[u] check), because a vertex must be marked visited before any vertices can be pushed onto the stack above it, and recursion stops when a vertex is encountered which has already been marked visited. Therefore, DFS requires 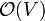 additional memory, and can be called "linear space". In practice this is often less than the memory used to store the graph in the first place, if the graph is explicit (
additional memory, and can be called "linear space". In practice this is often less than the memory used to store the graph in the first place, if the graph is explicit (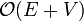 space with an adjacency list).
space with an adjacency list).
Non-recursive implementation
The less-preferred non-recursive implementation cannot be guaranteed to take only 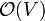 additional memory, since vertices are not visited immediately after being pushed on the stack (and therefore a vertex may be on the stack several times at any given moment). However, it is also clear that there can be no more than
additional memory, since vertices are not visited immediately after being pushed on the stack (and therefore a vertex may be on the stack several times at any given moment). However, it is also clear that there can be no more than 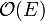 vertices on the stack at any given time, because every addition of a vertex to the stack is due to the traversal of an edge (except for that of the initial vertex) and no edge can be traversed more than twice. The stack space is therefore bounded by
vertices on the stack at any given time, because every addition of a vertex to the stack is due to the traversal of an edge (except for that of the initial vertex) and no edge can be traversed more than twice. The stack space is therefore bounded by 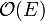 , and it is easy to see that a complete graph does indeed meet this upper bound.
, and it is easy to see that a complete graph does indeed meet this upper bound. 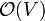 space is also required to store the list of visited vertices, so
space is also required to store the list of visited vertices, so 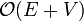 space is required overall.
space is required overall.
The DFS tree
Running DFS on a graph starting from a vertex from which all other vertices are reachable produces a depth-first spanning tree or simply DFS tree, because every vertex is visited and no vertex is visited on more than one path from the root (starting vertex). Depth-first spanning trees tend to be tall and slender, because DFS tends to always keep going along one path until it cannot go any further, and, hence, produce relatively long paths. The DFS tree has a number of useful properties that allow efficient solutions to important problems (see the Applications section).
Undirected graphs
When we run DFS on an undirected graph, we generally consider it as a directed graph in which every edge is bidirectional. (This is akin to adding an arrowhead to each end of each edge in a diagram of the graph using circles and line segments.) Running DFS on this graph selects some of the edges (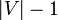 of them, to be specific) to form the spanning tree. Note that these edges point generally away from the source. They are known as tree edges. When we traverse a tree link, we make a recursive call to a previously unvisited vertex. The directed edges running in the reverse direction - from a node to its parent in the DFS tree - are known as parent edges, for obvious reasons. They correspond to a recursive call reaching the end of the function and returning to the caller. The remaining edges are all classified as either down edges or back edges. If a edge points from a node to one of its descendants in the spanning tree rooted at the source vertex, but it is not a tree edge, then it is a down edge; otherwise, it points to an ancestor, and if it is not a parent edge then it is a back edge. In the recursive implementation given, encountering either a down edge or a back edge results in an immediate return as the vertex has already been visited. Evidently, the reverse of a down edge is always a back edge and vice versa.
of them, to be specific) to form the spanning tree. Note that these edges point generally away from the source. They are known as tree edges. When we traverse a tree link, we make a recursive call to a previously unvisited vertex. The directed edges running in the reverse direction - from a node to its parent in the DFS tree - are known as parent edges, for obvious reasons. They correspond to a recursive call reaching the end of the function and returning to the caller. The remaining edges are all classified as either down edges or back edges. If a edge points from a node to one of its descendants in the spanning tree rooted at the source vertex, but it is not a tree edge, then it is a down edge; otherwise, it points to an ancestor, and if it is not a parent edge then it is a back edge. In the recursive implementation given, encountering either a down edge or a back edge results in an immediate return as the vertex has already been visited. Evidently, the reverse of a down edge is always a back edge and vice versa.
Every (directed) edge in the graph must be classifiable into one of the four categories: tree, parent, down, or back. To see this, suppose that the edge from node A to node B in some graph does fit into any of these categories. Then, in the spanning tree, A is neither an ancestor nor a descendant of B. This means that the lowest common ancestor of A and B in the spanning tree (which we will denote as C) is neither A nor B. Evidently, C is visited before either A or B, and A and B lie in different subtrees rooted at immediate children of C. So at some point C has been visited but none of its descendants have been visited. Now, because DFS always visits an entire subtree of the current vertex before backtracking and entering another subtree, the entire subtree containing either A or B (whichever one is visited first) must be explored before visiting the subtree containing the other. Suppose the subtree containing A is visited first. Then, when A is visited, B has not yet been visited, and thus the edge between them must be a tree edge, which is a contradiction.
Notice that given some graph, it is not possible to assign each edge a fixed classification. For example, in the complete graph of two vertices (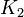 ), two of the (undirected) edges will be tree/parent, and the other one will be down/back, but which are which depends on the starting vertex and the order in which vertices are visited. Thus, when we say that a particular edge in the graph is a tree edge (or a parent, down, or back link), it is assumed that we are referring to the classification induced by a specific invocation of DFS on that graph. The beauty of DFS-based algorithms is that any valid edge classification (that is, edge classification produced by any correct invocation of DFS) is useful.
), two of the (undirected) edges will be tree/parent, and the other one will be down/back, but which are which depends on the starting vertex and the order in which vertices are visited. Thus, when we say that a particular edge in the graph is a tree edge (or a parent, down, or back link), it is assumed that we are referring to the classification induced by a specific invocation of DFS on that graph. The beauty of DFS-based algorithms is that any valid edge classification (that is, edge classification produced by any correct invocation of DFS) is useful.
Directed graphs
In directed graphs, edges are also classified into four categories. Tree edges, back edges, and down edges are classified just as they are in undirected graphs. There are no longer parent edges. If an tree edge exists from A to B, this does not guarantee the existence of an edge from B to A; if this edge does exist, it is considered a back edge, since it points from a node to its ancestor in the spanning tree. However, it is not true in a directed graph that every edge must be either tree, back, or down. In the sketch proof given for the corresponding fact in an undirected graph, we use the fact that it doesn't matter if A or B is visited first, since edges are bidirectional. But in the same circumstances in a directed graph, if there is an edge from A to B but no edge from B to A, and the subtree containing B is visited first, then the edge A-B is not a tree edge, since B has already been visited at the time that A is visited. Thus, when performing DFS on a directed graph, it is possible for an edge to lead from a vertex to another vertex which is neither a descendant nor an ancestor. Such an edge is called a cross edge. Again, these labels become meaningful only after DFS has been run.
Traversal of the spanning tree
In order to classify edges as tree, parent, down, back, or cross, we need to know which nodes are descendants of which. In effect, we would like to be able to answer the question "what is the relationship between nodes X and Y?", preferably in constant time per query (giving an optimal algorithm). The simplest way to do this, which is useful for other algorithms as well, is by preorder and postorder numbering of the nodes. In these numberings, nodes are assigned consecutive increasing integers (usually starting from 0 or 1). In preorder, a node is numbered as soon as it is visited: that is, the numbering of a node occurs pre-recursion, before any other nodes are visited. In postorder, a node is numbered after all the recursive calls arising from tree edges out of it have terminated - it occurs post-recursion. Here is code that assigns both preordering and postordering numbers at once. (Notice that we must visit vertices in the same order when assigning preordering and postordering numbers, otherwise the classification scheme for edges in a directed graph will fail. The best way to ensure that they are visited in the same order in both DFSs is by combining them into a single DFS.)
function DFS(u)
if pre[u] = ∞
pre[u] = precnt
precnt = precnt + 1
for each v ∈ V(G) such that (u,v) ∈ E(G)
DFS(v)
post[u] = postcnt
postcnt = postcnt + 1
input G
for each u ∈ V(G)
let pre[u] = ∞
let post[u] = ∞
let precnt=0
let postcnt=0
for each u ∈ V(G)
DFS(u)
Before a node has had a preorder or postorder number assigned, its number is ∞. At the termination of the algorithm, precnt=postcnt=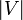 .
.
Classification of edges in undirected graphs
In an undirected graph, preorder numbers may be used to distinguish between down edges and back edges. (It becomes obvious when an edge is a tree edge or a parent edge, while running DFS, of course.) If node A has a higher preorder number than node B, then B is an ancestor and the edge is a back edge. Otherwise, the edge is a down edge.
Classification of edges in directed graphs
The situation is more complicated in directed graphs. Again it is obvious when an edge is a tree edge. Otherwise, consider the other possible classifications for an edge from A to B. If A is a descendant of B (back edge), then A has a higher preorder number but lower postorder number than B. If A is an ancestor of B (down edge), then A has a lower preorder number but higher postorder number than B. Finally, if A is neither an ancestor nor a descendant of B (cross edge), then an edge doesn't exist from B to A and B was visited before A, so A has a higher preorder number and a higher postorder number.
Note that we do not actually know the postorder number for a vertex until after we have examined all the edges leaving it. This is not a problem for the sake of classification, since we know that any number that hasn't been assigned yet is higher than any number that has been so far assigned, and that using ∞ as a placeholder therefore doesn't change the results of comparisons. You could also use -1 as a placeholder, but you would have to modify the code somewhat.
Topological sort
A topological ordering of a DAG can be obtained by reversing the postordering. A proof of this fact is given in the Topological sorting article.
Applications
DFS, by virtue of being a subcategory of graph search, is able to find connected components, paths (including augmenting paths), spanning trees, and topological orderings in linear time. The special properties of DFS trees also make it uniquely suitable for finding biconnected components (or bridges and articulation points) and strongly connected components. There are three well-known algorithms for the latter, those of Tarjan, Kosaraju, and Gabow. The classic algorithm for the former appears to have no unique name in the literature.
The following example shows how to find connected components and a DFS forest (a collection of DFS trees, one for each connected component).
function DFS(u,v)
if id[v] = -1
id[v] = cnt
let pred[v] = u
for each w ∈ V(G) such that (v,w) ∈ E(G)
DFS(v,w)
input G
cnt = 0
for each u ∈ V(G)
let id[u] = -1
for each u ∈ V(G)
if id[u] = -1
DFS(u,u)
cnt = cnt + 1
After the termination of this algorithm, cnt will contain the total number of connected components, id[u] will contain an ID number indicating the connected component to which vertex u belongs (an integer in the range [0,cnt)) and pred[u] will contain the parent vertex of u in some spanning tree of the connected component to which u belongs, unless u is the first vertex visited in its component, in which case pred[u] will be u itself.
Flood fill
The flood fill problem is often used as an example application of DFS. It avoids some of the implementational complexity associated with graph-theoretic algorithms by using an implicitly defined graph; there is no need to construct an adjacency matrix or adjacency list or any other such structure. Instead, we can just identify each vertex—a square in the grid—by its row and column indices; and it is very easy to find the adjacent squares. This is what a typical recursive implementation looks like (C++):
// (dx[i], dy[i]) represents one of the cardinal directions const int dx[4] = {0, 1, 0, -1}; const int dy[4] = {1, 0, -1, 0}; void do_flood_fill(vector<vector<int> >& grid, int r, int c, int oldval, int newval) { // invalid coordinates if (r < 0 || c < 0 || r >= grid.size() || c >= grid[0].size()) return; // outside the blob if (grid[r][c] != oldval) return; grid[r][c] = newval; for (int i = 0; i < 4; i++) do_flood_fill(grid, r + dx[i], c + dy[i], oldval, newval); } void flood_fill(vector<vector<int> >& grid, int r, int c, int newval) { if (grid[r][c] != newval) do_flood_fill(grid, r, c, grid[r][c], newval); }
References
- Sedgewick, Robert (1983). Algorithms (1st ed.). Addison-Wesley. ISBN 0-201-06672-6.