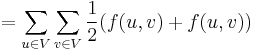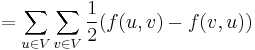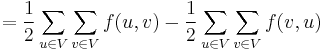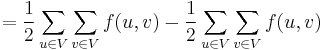Maximum flow
The maximum flow problem is an optimization problem in graph theory. It deals with a special kind of graph, known as a flow network.
Contents
The flow network
A flow network is a directed graph with the following properties:
- There are two special nodes, the source (usually denoted s), and the sink (usually denoted t).
- No edges enter the source nor leave the sink.
- To each edge we associate a non-negative real number called the capacity. Thus, we can represent a flow network similarly to how we would represent a weighted graph.
We may describe a flow network mathematically as a tuple 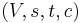 where
where 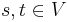 ,
, 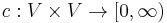 , and
, and 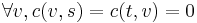 . Here
. Here 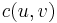 is the capacity of the edge from
is the capacity of the edge from  to
to  . When we talk about an edge in a flow network, we are talking about an ordered pair of vertices
. When we talk about an edge in a flow network, we are talking about an ordered pair of vertices 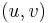 for which
for which 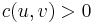 . That is, we say that an edge exists from
. That is, we say that an edge exists from  to
to  if and only if
if and only if 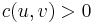 .
.
A flow network may be used to model real-life systems in which some substance flows from one place (the source) to another (the sink), going through any number of intermediate locations (other nodes) along paths of various maximum capacities connecting locations (edges). This is the motivation behind the statement of the maximum flow problem.
Admissible flows
In order to state the maximum flow problem, we must first define the concept of an admissible flow. We have a flow network, and this flow network has a capacity function that represents, in some sense, the maximum rate at which flow can occur between a given pair of vertices. An admissible flow is an actual choice of how much flow to send between each pair of vertices. Of course, this cannot exceed the capacity. Furthermore, sending  units of flow from vertex
units of flow from vertex  to vertex
to vertex  is equivalent to sending
is equivalent to sending 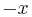 units of flow from vertex
units of flow from vertex  to vertex
to vertex  . Finally, flow is not allowed to "accumulate" at a vertex; the amount flowing in must equal the amount flowing out.
. Finally, flow is not allowed to "accumulate" at a vertex; the amount flowing in must equal the amount flowing out.
Mathematically, an admissible flow is a function 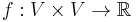 such that:
such that:
- Capacity constraint:
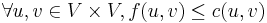 .
. - Skew symmetry:
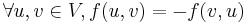 .
. - Conservation of flow:
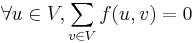 .
.
Note that the conservation constraint is more naturally translated as 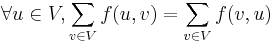 based on our description above ("the amount flowing in must equal the amount flowing out"). However, as a consequence of the skew symmetry constraint,
based on our description above ("the amount flowing in must equal the amount flowing out"). However, as a consequence of the skew symmetry constraint, 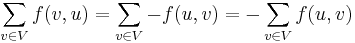 . If this is to equal
. If this is to equal 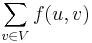 , then this quantity must be identically zero.
, then this quantity must be identically zero.
An edge 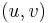 and its reverse edge
and its reverse edge 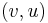 may have different capacities. For example, if
may have different capacities. For example, if 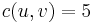 and
and 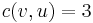 , then we can, for example, send 4 units of flow from
, then we can, for example, send 4 units of flow from  to
to  and -4 units from
and -4 units from  to
to  . (Negative flow always satisfies a capacity constraint.) We cannot send 4 units of flow from
. (Negative flow always satisfies a capacity constraint.) We cannot send 4 units of flow from  to
to  and -4 units from
and -4 units from  to
to  , however, because
, however, because 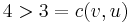 . If positive flow goes from
. If positive flow goes from  to
to  , we can only send up to 3 units. We also cannot send 5 units from
, we can only send up to 3 units. We also cannot send 5 units from  to
to  and 3 units from
and 3 units from  to
to  , because this violates skew symmetry.
, because this violates skew symmetry.
In the remainder of this article, flow will mean admissible flow when the context is appropriate.
Analogies
- In one possible analogy, the edges represent pipes, each of which has some maximum rate at which it can transport water (the capacity). An admissible flow then corresponds to some way of sending water through the pipes from source to sink through a series of intermediate nodes. The rate at which water flows into an intermediate node must equal the rate at which water flows out of the same node, because the nodes can't store excess water, and water can't just come out of nowhere.
- In another possible analogy, the edges represent conducting wires, each of which has some maximum amount of current it can conduct before it overheats and melts; the source represents a generator and the sink represents a device that consumes electrical power. Here, the balance condition is Kirchhoff's current law, stating that the total current flowing into a vertex equals the total current flowing out of it, and corresponds to the fact that any imbalance in current would result in an accumulation of either positive or negative charge at that vertex. In this analogy, the role of skew symmetry is clearer. In circuit analysis, sending a positive current from one node to another is equivalent to sending the same amount of negative current in the other direction.
Residual network
Given a flow network 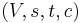 and a flow
and a flow  , we may form the residual capacity network or simply residual network
, we may form the residual capacity network or simply residual network 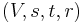 . This is a new flow network in which
. This is a new flow network in which 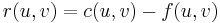 . Because
. Because 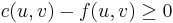 for any valid flow,
for any valid flow,  is a valid capacity function (takes on nonnegative values only). The residual network may contain edges that the original network does not. In particular, if
is a valid capacity function (takes on nonnegative values only). The residual network may contain edges that the original network does not. In particular, if 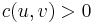 and
and 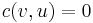 , and we send flow from
, and we send flow from  to
to  in
in  , that is,
, that is, 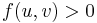 , then
, then 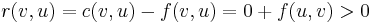 . In other words, sending flow in one direction between two vertices can generate a back edge in the residual network. If a reverse edge already existed, then sending flow along the forward edge causes the capacity of the reverse edge to increase in the residual network.
. In other words, sending flow in one direction between two vertices can generate a back edge in the residual network. If a reverse edge already existed, then sending flow along the forward edge causes the capacity of the reverse edge to increase in the residual network.
The residual network tells us how much capacity is left in the original flow network after we've already sent some flow through it. The appearance of back edges corresponds to the fact that we are now allowed to send flow in the other direction to cancel out the existing flow. For example, if 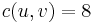 and
and 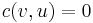 , and
, and 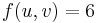 , then
, then 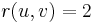 and
and 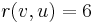 . We can send further flow of up to 2 units in the
. We can send further flow of up to 2 units in the  to
to  direction, or we can send flow from
direction, or we can send flow from  to
to  of up to 6 units. As long as we do not send more than 6 units in the
of up to 6 units. As long as we do not send more than 6 units in the  to
to  direction, this will just cancel out the existing flow and the total flow from
direction, this will just cancel out the existing flow and the total flow from  to
to  will still be less than or equal to zero, which makes the flow valid for the original network.
will still be less than or equal to zero, which makes the flow valid for the original network.
Statement of the problem
Given an admissible flow, although incoming flow and outgoing flow balance at all vertices other than the source and the sink, the same is not true at the source and sink. Indeed, we can have flow out from the source, but not in, since no edges enter the source; we can have flow into the sink but not out, since no edges leave the sink. The objective of the problem is to find an admissible flow that maximizes the total flow out of the source or into the sink. Such a flow is called a maximum flow.
Proposition: The total outgoing flow at the source equals the total incoming flow at the sink.
Proof: Consider the total outgoing flow at all vertices, 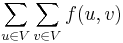 . This is zero by skew symmetry. Explicitly:
. This is zero by skew symmetry. Explicitly:
where, between the third-to-last and second-to-last lines, we have relabelled the dummy variables  and
and  in the second term and exchanged the order of summation.
in the second term and exchanged the order of summation.
We now rewrite the original sum as 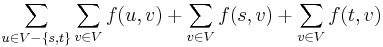 . The first term is zero, by the conservation constraint. The entire expression also equals zero. Therefore
. The first term is zero, by the conservation constraint. The entire expression also equals zero. Therefore 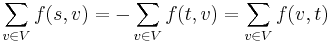 , which is what we wanted.
, which is what we wanted. 
This common value is called the value of the flow. This is what we wish to maximize in the maximum flow problem.
Algorithms
There are a variety of algorithms for finding a maximum flow in a flow network. The simplest are the Ford–Fulkerson method and the preflow push algorithms.
Ford–Fulkerson method
The Ford–Fulkerson method (q.v.) comprises a set of algorithms that each proceed in a series of steps, gradually building up an admissible flow until it has reached its maximum value. Each step of the algorithm takes the previous step's output, an admissible flow, as input, and produces an admissible flow of greater value, until no further refinement is possible. The input for the first step is the empty flow (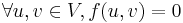 ), which is always admissible. The refinement is done by finding an s-t path in the flow network that can be "added" to the current admissible flow, called an augmenting path. In subsequent stages, we find an augmenting path in the residual network rather than the original network. Once an augmenting path can no longer be found in the residual network, the network is saturated with flow and the algorithm terminates.
), which is always admissible. The refinement is done by finding an s-t path in the flow network that can be "added" to the current admissible flow, called an augmenting path. In subsequent stages, we find an augmenting path in the residual network rather than the original network. Once an augmenting path can no longer be found in the residual network, the network is saturated with flow and the algorithm terminates.
There is flexibility in how to choose the augmenting path at each step. A simple approach is to always pick the path with the fewest edges; this gives the Edmonds–Karp algorithm. A faster and more sophisticated approach involves partitioning the graph into level sets by distance from the source and only considering paths in which each edge proceeds from a level to the next. This is called Dinic's algorithm.
Preflow push algorithms
Preflow push algorithms differ from augmenting path algorithms in that they do not maintain an admissible flow in each step, but instead maintain a preflow, in which the total flow entering a vertex is allowed to exceed the total flow exiting the vertex (but not vice versa). The algorithm begins by generating a preflow in which every edge leaving the source is saturated (so that the source's neighbours all have excess incoming flow). Each step of the algorithm then attempts to discharge some vertex's excess by pushing flow from that vertex to an adjacent vertex. Some flow will be discharged into the sink, and whatever flow cannot be discharged into the sink eventually finds its way back to the source. The algorithm terminates when the intermediate vertices have completely discharged all of their excess incoming flow, and thus an admissible flow has been found.
Other approaches
The max flow problem may be expressed as a linear program and solved using the techniques of linear programming. Here the vector to be optimized corresponds to the flow  , and has one entry for each edge in the graph. Both the capacity constraints and the balance condition are linear, and may be expressed in the form
, and has one entry for each edge in the graph. Both the capacity constraints and the balance condition are linear, and may be expressed in the form 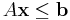 . The value of the flow is also a linear function of the vector
. The value of the flow is also a linear function of the vector 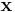 . Details are left as an exercise for the reader.
. Details are left as an exercise for the reader.
Even more sophisticated approaches were given by King, Rao, and Tarjan (1994) and Orlin (2012). Combining the two approaches gives a lower bound of 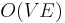 on the general max flow problem, the best known to date.
on the general max flow problem, the best known to date.
Minimum s-t cut problem
Given a directed graph with two special nodes, the source s (with all edges outgoing) and the sink t (with all edges incoming), we can define an s-t cut as a subset of edges that, when removed from the graph, leave the sink unreachable from the source. For example, if there is no path from the source to the sink in the original graph, then the empty set is a valid s-t cut (as are all other subsets of 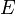 ).
).
If the graph is weighted, then we may ask for a minimum s-t cut, that is, an s-t cut whose total weight (sum of the weights of the edges it comprises) is as small as possible. We will refer to such a graph as a weighted s-t graph and represent it as 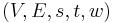 with
with 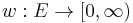 representing the edge weights. Negative-weight edges are not allowed for simplicity, but it is easy to handle them: it is always better to cut them than not to cut them, so we remove them from the graph immediately.
representing the edge weights. Negative-weight edges are not allowed for simplicity, but it is easy to handle them: it is always better to cut them than not to cut them, so we remove them from the graph immediately.
A common analogy is bombing enemy supply lines. Here, there is a set of one-way roads (edges) and warehouses (vertices) used to transport materials from some factory (the source) to the front lines (the sink). Each road has a certain cost to bomb (its weight), and we want to bomb enough roads to disconnect the factory from the front lines, while minimizing total cost.
For any weighted s-t graph 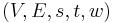 , there is a corresponding flow network
, there is a corresponding flow network 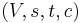 with the same structure. Here,
with the same structure. Here, 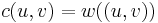 if
if 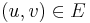 , otherwise
, otherwise 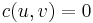 . In other words, the capacity between two vertices in the flow network is just the weight of the edge between them in the weighted s-t graph, or zero if there is no such edge.
. In other words, the capacity between two vertices in the flow network is just the weight of the edge between them in the weighted s-t graph, or zero if there is no such edge.
A famous result known as the max-flow min-cut theorem demonstrates the equivalence of the maximum flow and minimum s-t cut problems. The theorem tells us that the value of a max flow in a flow network equals the total weight of a min cut in the corresponding weighted s-t graph. Because of this, there is no need to devise separate algorithms for the max flow and minimum s-t cut problems. Constructing a min cut from a max flow is straightforward and is based on the proof of the theorem. On the other hand, a max flow cannot be straightforwardly constructed from a min cut.
Variations
One or more edges in a flow network may be uncapacitated. Such an edge has unlimited capacity. We can usually handle such edges by setting their capacity to a very large value, greater than the sum of capacities of all capacitated edges in the graph. An uncapacitated edge in a flow network corresponds to an uncuttable edge in a weighted s-t graph.
Sometimes we may have to deal with a variation of a flow network in which there may be multiple sources or multiple sinks. This can be handled by adding a new "supersource" with an uncapacitated edge to each of the original sources. Likewise, we can add a new "supersink" with an uncapacitated edge from each of the original sinks.
A flow network in which there are multiple edges between a given pair of vertices can be handled by replacing the multiple edges by a single edge whose capacity equals the sum of the capacities of the original edges.
The maximum flow problem is easily solved when there are vertex capacities in addition to edge capacities. A vertex capacity 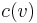 is the constraint that
is the constraint that 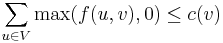 ; in other words, the total amount of incoming positive flow (or, equivalently, outgoing positive flow) cannot exceed the capacity. We can always reduce a network with vertex capacities to a network with only edge capacities and hence solve the problem using any standard max flow algorithm on the result of the reduction. To do so, we split each vertex
; in other words, the total amount of incoming positive flow (or, equivalently, outgoing positive flow) cannot exceed the capacity. We can always reduce a network with vertex capacities to a network with only edge capacities and hence solve the problem using any standard max flow algorithm on the result of the reduction. To do so, we split each vertex  into an "incoming vertex"
into an "incoming vertex" 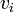 and an "outgoing vertex"
and an "outgoing vertex" 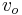 . Every edge
. Every edge 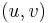 in the original network is mapped to the edge
in the original network is mapped to the edge 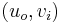 in the new network (i.e., an edge leaving the outgoing vertex of
in the new network (i.e., an edge leaving the outgoing vertex of  and entering the incoming vertex of
and entering the incoming vertex of  ) of the same capacity. Furthermore, we add an edge from
) of the same capacity. Furthermore, we add an edge from 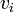 to
to 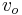 whose capacity equals the original vertex capacity
whose capacity equals the original vertex capacity 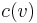 . In such a way, all flow that would have gone through
. In such a way, all flow that would have gone through  in the original graph must now enter through
in the original graph must now enter through 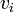 and exit through
and exit through 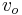 , going through the edge
, going through the edge 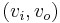 ; a constraint on this edge therefore yields the desired result, effectively a constraint on the original vertex.
; a constraint on this edge therefore yields the desired result, effectively a constraint on the original vertex.
We can likewise consider the minimum s-t cut problem in which we are allowed to remove vertices (for a cost) as well as edges. The reduction is analogous: we split each vertex into an incoming vertex and an outgoing vertex, with an edge from the incoming vertex to the outgoing vertex whose weight equals the original vertex cost.
Applications
TODO