Augmenting path
An augmenting path in a flow network is a path from the source to the sink in the residual network for some flow. It is so named because it is possible to augment (increase) the value of the flow by combining the existing flow with additional flow along the augmenting path.
Augmenting a flow
Let 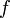 be a flow in the flow network
be a flow in the flow network 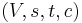 . Let
. Let 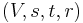 be the residual network corresponding to
be the residual network corresponding to 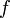 . Now consider an augmenting path
. Now consider an augmenting path 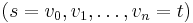 in the residual network. We will assume that the augmenting path is simple. Since edges must have positive capacity, the minimum residual capacity along all arcs on the augmenting path,
in the residual network. We will assume that the augmenting path is simple. Since edges must have positive capacity, the minimum residual capacity along all arcs on the augmenting path, 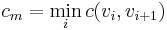 , is positive.
, is positive.
We define the augmented flow 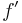 as follows:
as follows: 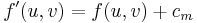 if the edge
if the edge 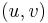 is in the augmenting path;
is in the augmenting path; 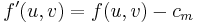 if the reverse edge
if the reverse edge 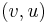 is in the augmenting path, and, otherwise,
is in the augmenting path, and, otherwise,  .
.
Proposition: The augmented flow 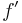 is an admissible flow. Furthermore,
is an admissible flow. Furthermore, 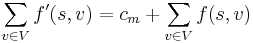 ; that is, the augmented flow's value is greater than the original flow's value by
; that is, the augmented flow's value is greater than the original flow's value by 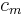 .
.
Proof:
- Capacity. If
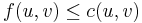 , then clearly
, then clearly 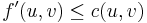 whenever
whenever 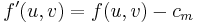 or
or  . We only need to check the case
. We only need to check the case 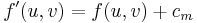 . In this case,
. In this case, 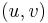 is an edge in the augmenting path. By definition of
is an edge in the augmenting path. By definition of 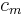 , we have that
, we have that 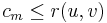 . Therefore
. Therefore 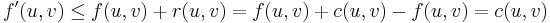 , as required.
, as required. - Skew symmetry. Let
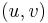 be an edge. If
be an edge. If 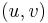 is an edge in the augmenting path, then
is an edge in the augmenting path, then 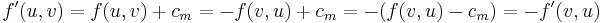 . If on the other hand
. If on the other hand 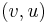 is in the augmenting path, then
is in the augmenting path, then 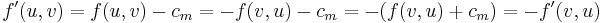 . If neither is true, then
. If neither is true, then 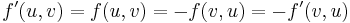 .
. - Flow conservation: Let
 be a vertex other than the source or sink. If
be a vertex other than the source or sink. If  is not in the augmenting path, then all flows into
is not in the augmenting path, then all flows into  are unchanged, and conservation is maintained. If
are unchanged, and conservation is maintained. If  is in the augmenting path, then (since
is in the augmenting path, then (since 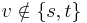 ) it must be preceded by a vertex
) it must be preceded by a vertex 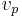 and followed by a vertex
and followed by a vertex 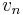 in the augmenting path. Then
in the augmenting path. Then 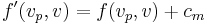 ,
, 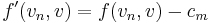 , and all other flows into
, and all other flows into  are unchanged. Since one inward flow is incremented and another decremented by the same amount, conservation is maintained.
are unchanged. Since one inward flow is incremented and another decremented by the same amount, conservation is maintained.
Finally, consider the value of the augmented flow, 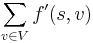 . The source is always the first vertex in the augmenting path. Thus,
. The source is always the first vertex in the augmenting path. Thus, 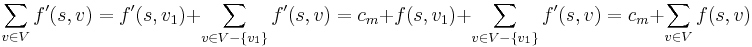 .
. 
Intuitively, augmenting the flow corresponds to "pushing additional flow" along the augmenting path using residual capacity. The augmented flow is then the overall result of pushing both the original flow and the additional flow.
Augmenting path theorem
It is now clear that a flow cannot be maximal as long as an augmenting path exists, as we can increase the flow by pushing along the augmenting path. The converse is less clear: if the flow is not maximal, then an augmenting path exists. This is the topic of this section.
Theorem (Augmenting path theorem): Let 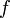 be a flow in the flow network
be a flow in the flow network 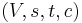 . Then
. Then 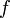 is maximal if and only if there is no augmenting path in the residual network
is maximal if and only if there is no augmenting path in the residual network 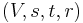 .
.
Proof: The "only if" direction is easy. The proof of the "if" direction is based on the max-flow min-cut theorem. Since there is no augmenting path, we can form the set 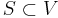 of vertices reachable from
of vertices reachable from  in the residual network. As in the max-flow min-cut theorem,
in the residual network. As in the max-flow min-cut theorem, 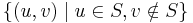 forms an s-t cut of the weighted s-t graph corresponding to the original flow network, whose total weight equals the value of the flow
forms an s-t cut of the weighted s-t graph corresponding to the original flow network, whose total weight equals the value of the flow 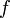 . Since every flow's value is less than or equal to every cut's total weight,
. Since every flow's value is less than or equal to every cut's total weight, 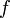 must be maximal.
must be maximal. 
The augmenting path theorem forms the theoretical basis of the Ford–Fulkerson method for computing a max flow.