Kruskal's algorithm
Kruskal's algorithm is a general-purpose algorithm for the minimum spanning tree problem, based on the disjoint sets data structure. The existence of very simple algorithms to maintain disjoint sets in almost constant time gives rise to simple implementations of Kruskal's algorithm whose running times are close to linear, usually outperforming Prim's algorithm in sparse graphs.
Contents
Theory of the algorithm
Kruskal's may be characterized as a greedy algorithm, which builds the MST one edge at a time. As befits a MST algorithm, the greedy strategy is to continually add the remaining edge of lowest weight. Unlike Prim's, however, Kruskal's adds edges without regard to the connectivity of the partially built MST. We shall assume that a spanning tree exists for the following sections. (If you find them too difficult, skip them.)
Lemma
Suppose that a spanning tree  is given of some graph
is given of some graph  . Then, the addition of any edge
. Then, the addition of any edge 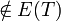 to
to 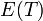 , followed by the removal of any edge from the resulting cycle, yields a spanning tree of
, followed by the removal of any edge from the resulting cycle, yields a spanning tree of  .
.
Proof: Before the operation, the number of vertices is one more than the number of edges. After the operation, this is again true. As the addition of the new edge generates exactly one simple cycle, there are no longer any cycles after an edge on this cycle is removed. So the new  has a vertex count which exceeds its edge count by one and contains no cycles; it must therefore be a tree.
has a vertex count which exceeds its edge count by one and contains no cycles; it must therefore be a tree.
The algorithm
We are now ready to present the algorithm. We begin with no knowledge of the edges of the MST, and add them one by one until the MST is complete. To do so we consider edges in increasing order of weight. When considering an edge, if adding it would create a cycle, we skip it; otherwise we add it. Once 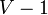 edges have been added, we have constructed a MST. Kruskal's is both correct (Theorem 2) and complete (Theorem 1).
edges have been added, we have constructed a MST. Kruskal's is both correct (Theorem 2) and complete (Theorem 1).
Remark
If adding an edge to the partially built MST generates a cycle, it will also do so if the edge is added to the partially built MST later on in the algorithm, since we only add edges and never remove them. The contrapositive is also true: if adding an edge does not generate a cycle, it wouldn't have generated a cycle if it were added earlier, either.
Theorem 1
Kruskal's algorithm will never fail to find a spanning tree in a connected graph.
Proof: By contradiction. Assume that all edges have been considered and the partially built tree is still not complete. Then, there exists some edge that connects two vertices in different connected components of the partially built tree. But this edge must have been considered at some point and discarded as adding it would have created a cycle. This is a contradiction, as adding it now would not create a cycle, per the Remark above.
Theorem 2
Kruskal's algorithm will never produce a non-minimal spanning tree.
Proof:
We first proceed by induction on the number of edges so far added.
- When no edges have yet been added, the set of edges so far added, being empty, is obviously a subset of the edges of some MST.
- Suppose that
 edges have been added in this manner (
edges have been added in this manner (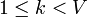 ), and we know that they form a subset
), and we know that they form a subset  of the edges of some MST. All further edges to be considered are of greater or equal weight. If adding an edge generates a cycle at this point, it can be discarded, as it can never be added per the Remark above. According to our algorithm, then, the next edge to be added is the edge
of the edges of some MST. All further edges to be considered are of greater or equal weight. If adding an edge generates a cycle at this point, it can be discarded, as it can never be added per the Remark above. According to our algorithm, then, the next edge to be added is the edge  with minimal weight which does not generate a cycle. Consider now any MST
with minimal weight which does not generate a cycle. Consider now any MST  containing the edges so far added as a subset of its edge set. It it contains
containing the edges so far added as a subset of its edge set. It it contains  , we are done; we know that when
, we are done; we know that when  is added our edge set is still a subset of the edge set of some MST. Otherwise, add the edge
is added our edge set is still a subset of the edge set of some MST. Otherwise, add the edge  to
to 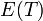 . A cycle is now generated. This cycle must contain some edge not yet considered, because we know that the edge currently under consideration, in conjunction with the edges previously added, do not form a cycle. This edge not yet considered has a weight greater than or equal to that of
. A cycle is now generated. This cycle must contain some edge not yet considered, because we know that the edge currently under consideration, in conjunction with the edges previously added, do not form a cycle. This edge not yet considered has a weight greater than or equal to that of  . Then, deleting this edge yields a new spanning tree (per the Lemma above). If the edge deleted was of greater weight than
. Then, deleting this edge yields a new spanning tree (per the Lemma above). If the edge deleted was of greater weight than  , the resulting spanning tree has lower weight than
, the resulting spanning tree has lower weight than  , a contradiction as
, a contradiction as  was assumed to be minimal. Otherwise, it must have equal weight to
was assumed to be minimal. Otherwise, it must have equal weight to  , and deleting it and adding
, and deleting it and adding  gives a new spanning tree of equal weight, that is, another MST. So we have proven that given that there is any MST at all containing
gives a new spanning tree of equal weight, that is, another MST. So we have proven that given that there is any MST at all containing  , we can add
, we can add  and find some MST containing this new set as a subset of its own edge set.
and find some MST containing this new set as a subset of its own edge set.
Implementation
We have so far glossed over a crucial detail: we must have a means of efficiently deciding whether an edge can be added without generating a cycle, and of adding that edge if it can. To do so, we note that a cycle is created if and only if the two endpoints of the edge are in the same connected component. We could, of course, answer this query through any graph search algorithm such as DFS or BFS. However, that would make the algorithm quadratic time overall, which is undesirable. Instead, we notice that a data structure already exists which can efficiently identify the component containing a vertex and add new edges (joining together components). Assuming that we know how to implement it, then, here is Kruskal's algorithm:
input G
let T = (V(G),∅)
for each {u,v} ∈ E(G) in increasing order of wt(u,v)
if find(u) ≠ find(v)
unite(u,v)
add {u,v} to E(T)
It would make sense to stop the loop after 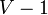 edges have been added (instead of processing every edge, which is often unnecessary). Nevertheless, it does not affect the asymptotic complexity (see Analysis)
edges have been added (instead of processing every edge, which is often unnecessary). Nevertheless, it does not affect the asymptotic complexity (see Analysis)
Analysis
The usual implementation of Kruskal's sorts the edges by weight first, which takes 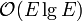 time. Following this,
time. Following this, 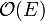 union-find operations are performed. As each can be done in almost-constant time (see the article itself), this step requires approximately
union-find operations are performed. As each can be done in almost-constant time (see the article itself), this step requires approximately 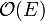 time to complete. The cost of the sort then dominates the running time. As typical implementations of quicksort, usually used here, are faster than those of heapsort, which may be said to operate implicitly in Prim's algorithm, a well-coded Kruskal's will outperform Prim's in sparse graphs. In dense graphs, Prim's non-heap implementation, taking
time to complete. The cost of the sort then dominates the running time. As typical implementations of quicksort, usually used here, are faster than those of heapsort, which may be said to operate implicitly in Prim's algorithm, a well-coded Kruskal's will outperform Prim's in sparse graphs. In dense graphs, Prim's non-heap implementation, taking 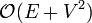 time, is likely to outperform Kruskals, with runtime close to
time, is likely to outperform Kruskals, with runtime close to 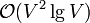 . In-place quicksort takes expected linear stack space, and the disjoint set data structure takes linear extra space, so Kruskal's has a linear memory complexity.
. In-place quicksort takes expected linear stack space, and the disjoint set data structure takes linear extra space, so Kruskal's has a linear memory complexity.
References
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 23.2: The algorithms of Kruskal and Prim, pp.567–574.