Prim's algorithm
Prim's algorithm (sometimes known as the Jarník-Prim algorithm) is one of the simplest and best-known minimum spanning tree algorithms. It is closely analogous to Dijkstra's algorithm, the only difference being that the length of each edge is minimized, rather than the total length of the path ending at each edge. Unlike Dijkstra's, Prim's can tolerate negative-weight edges with no difficulty. It is optimal for dense graphs; Kruskal's algorithm may perform better on sparse graphs. The precise time complexity of Prim's algorithm depends on the nature of the data structures used.
Contents
Theory of the algorithm
Prim's may be characterized as a greedy algorithm, which builds the MST one edge at a time, always branching out from the part of the tree currently built (and hence keeping the entire partial MST in one connected component, unlike Kruskal's), always adding the lowest-weight edge available. We assume below that a spanning tree exists (that the graph is fully connected). If you find the three sections below too difficult, skip them.
Lemma 1
Suppose that a spanning tree  is given of some graph
is given of some graph  . Then, the addition of any edge
. Then, the addition of any edge 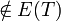 to
to 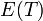 , followed by the removal of any edge from the resulting cycle, yields a spanning tree of
, followed by the removal of any edge from the resulting cycle, yields a spanning tree of  .
.
Proof: Before the operation, the number of vertices is one more than the number of edges. After the operation, this is again true. As the addition of the new edge generates exactly one simple cycle, there are no longer any cycles after an edge on this cycle is removed. So the new  has a vertex count which exceeds its edge count by one and contains no cycles; it must therefore be a tree.
has a vertex count which exceeds its edge count by one and contains no cycles; it must therefore be a tree.
Lemma 2
Given some tree  which is a subgraph of graph
which is a subgraph of graph  that is known to be a subtree of some MST of
that is known to be a subtree of some MST of  , we shall call an edge a crossing edge if it joins a vertex
, we shall call an edge a crossing edge if it joins a vertex 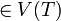 and a vertex
and a vertex 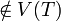 . Then, any minimal crossing edge
. Then, any minimal crossing edge  may be added to
may be added to  to give a new tree which is also a subtree of some MST of
to give a new tree which is also a subtree of some MST of  .
.
Proof: Given some MST of  containing
containing  as a subtree, we may add our minimal crossing
as a subtree, we may add our minimal crossing  to the MST. Evidently, the resulting cycle must contain another crossing edge. If this other crossing edge is of higher weight than
to the MST. Evidently, the resulting cycle must contain another crossing edge. If this other crossing edge is of higher weight than  , we can delete it to yield a new spanning tree, per Lemma 1, whose weight is lower than the weight of the original spanning tree, contradicting our assumption that the spanning tree with which we started was minimal. Otherwise, the other crossing edge is of the same weight as
, we can delete it to yield a new spanning tree, per Lemma 1, whose weight is lower than the weight of the original spanning tree, contradicting our assumption that the spanning tree with which we started was minimal. Otherwise, the other crossing edge is of the same weight as  (it cannot be of lower weight, since
(it cannot be of lower weight, since  is minimal) and the addition of
is minimal) and the addition of  and deletion of this edge yield, per Lemma 2, another spanning tree, this time of the same weight as the original, which is therefore another MST of
and deletion of this edge yield, per Lemma 2, another spanning tree, this time of the same weight as the original, which is therefore another MST of  . That is, given any MST of
. That is, given any MST of  that does not contain
that does not contain  , we are able to generate another that does.
, we are able to generate another that does.
The algorithm
The algorithm then operates as follows: we start with a trivial tree containing only one vertex (and no edges). It does not matter which vertex is chosen. Then, we choose a minimal-weight edge emanating from that vertex, adding it to our tree. We repeatedly choose a minimal-weight edge that joins any vertex in the tree to one not in the tree, adding the new edge and vertex to our tree. Such an edge will always exist when the tree is incomplete because otherwise the partially built tree would be an isolated component (and yet we know that the graph consists of a single connected component.) When there are no more vertices to add, the tree we have built is an MST.
Proof: By induction.
- Base case: We begin with a tree which, as it contains only one vertex and no edges, is certainly a subtree of some MST of the graph. (Of course, it is a subtree of all MSTs of the graph, but that fact is not important here.)
- Inductive step: By Lemma 2, if the current tree is the subtree of some MST of the graph, then the tree resulting from the addition of any minimal crossing edge to our tree yields a new tree which is also the subtree of some MST of the graph.
Implementation
As the previous sections are a bit heavy, here is some pseudocode for Prim's algorithm:
input G
let u = some vertex ∈ V(G)
let T = ({u},∅)
while V(T) ≠ V(G)
let (v,w) ∈ E(G) such that v ∈ V(T), w ∉ V(T), and wt(v,w) is minimal
add w to V(T)
add (v,w) to E(T)
Analysis
Note the close similarity between Prim's algorithm and Dijkstra's algorithm. Indeed, the running time bounds for Prim's algorithm match those of Dijkstra's algorithm. Using a simple array and iteration, 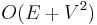 is attained; using a binary heap gives
is attained; using a binary heap gives 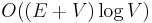 , which is better in sparse graphs, and using a Fibonacci heap gives
, which is better in sparse graphs, and using a Fibonacci heap gives 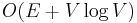 .
.
References
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 23.2: The algorithms of Kruskal and Prim, pp.567–574.