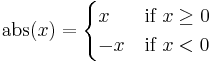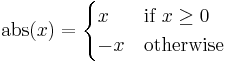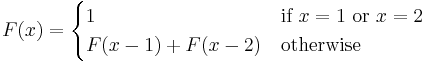Recursive function
Recursion is the property exhibited by entities that are defined in terms of themselves, that is, recur in themselves. In computer science, the most important recursive entities are recursively defined functions. Mathematical functions are usually thought of as sets of ordered pairs, the first element in the pair from the domain, the second from the range, and, hence, a function cannot be intrinsically recursive. However, functions in computer programs are instead defined in a form that allows computers to evaluate them (efficiently, it is hoped), and the definition of a function in a computer program may reference the function itself. Such a function, that occurs in its own definition, is said to be recursively defined, and, with the understanding that we are speaking of the definition of a function rather than its abstract mathematical essence, we will refer to them simply as recursive functions. The term recursion is then defined also as the process of evaluating recursive functions, and, by extension, the formulation of algorithms in terms of recursive functions.
Contents
Notation
In mathematics
Recursive functions are notated similarly to piecewise functions. An example of a piecewise function is the absolute value function:
To evaluate this function, we find the first line within the curly braces for which the condition on the right hand side is satisfied, and use the expression on the left hand side as the value. Thus, if 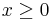 , then the value of
, then the value of 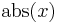 is
is  , whereas if
, whereas if 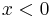 , then the value of
, then the value of 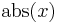 is instead
is instead 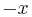 .
.
Often, the condition on the last line will be replaced with the word "otherwise". This is like the else condition in a case statement (switch in C and related languages); it is chosen when none of the preceding conditions are satisfied. Thus we could rewrite the above as
It is good form, but not strictly necessary, to make the conditions in the definition exhaustive and mutually exclusive, that is, exactly one condition should be true for each element in the domain. If they are not exhaustive, it is a sign that the domain was poorly specified, whereas if they are not mutually exclusive then it can be slightly confusing.
A recursive function is characterized by the recurrence of the function name in one or more of the left-hand expressions within the brace. Here is a classic example:
The domain of the function 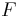 is
is 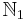 . We see that
. We see that 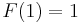 and
and 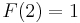 . To evaluate
. To evaluate 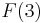 , we must use the "otherwise" clause, and hence we see that
, we must use the "otherwise" clause, and hence we see that
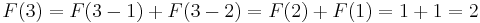
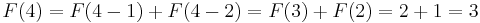
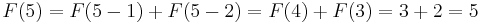
- (and so on)
The cases in the definition that call the defined function are called recursive cases; the "otherwise" line in the definition of 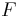 is the recursive case. Those that do not are called base cases; the line that defines
is the recursive case. Those that do not are called base cases; the line that defines 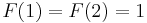 is the base case. Every recursive function has at least one recursive case (if it did not, it would not be called recursive) and at least one base case. This is because a recursive function definition without a base case would be an endlessly circular definition; attempting to evaluate the function would lead to endless or infinite recursion.
is the base case. Every recursive function has at least one recursive case (if it did not, it would not be called recursive) and at least one base case. This is because a recursive function definition without a base case would be an endlessly circular definition; attempting to evaluate the function would lead to endless or infinite recursion.
In code
Nearly all mainstream programming languages that support functions support recursive functions. (A language such as HTML is an obvious exception; it is intended to describe a document instead of a computation, and hence lacks functions altogether). In these languages, in any place in the code where a function calls another function, it can just as well call itself using the same notation. The code parallels the mathematical notation, for example:
C:
int F(int x) { if (x == 1 || x == 2) return 1; else // i.e., "otherwise" return F(x - 1) + F(x - 2); }
Haskell:
f :: Int -> Int f x | x == 1 || x == 2 = 1 | otherwise = f (x-1) + f (x-2)
(Note that function names are not allowed to start with uppercase letters in Haskell.)
Philosophy
Statement
Recursion is a powerful tool for solving problems, but it is not always obvious how to approach a problem recursively. The general principle, often called divide and conquer, is as follows:
Non-computer science examples
This philosophy is not restricted to computer science. Below we give some examples from other fields that may assist the reader in internalizing the divide and conquer philosophy and appreciating its ubiquity. When the solution to an instance requires the solutions to simpler instances, those simpler instances will be indented an additional level to show this relationship.
Problem: Climb a ladder. The generic form of this problem is Be at the top of the ladder. The instance is where you already are. Hence, climbing from the bottom to the top and climbing from the middle to the top are both the same problem, but different instances of it.
Solution: If you are already at the top, this is a trivial instance; you don't actually have to do anything. If you are not at the top, suppose there are  rungs remaining, where
rungs remaining, where 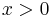 . Notice that the problem would be easier to solve if there were only
. Notice that the problem would be easier to solve if there were only 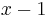 rungs separating you from the top of the ladder. So climb up one rung; this will reduce the instance at hand to an easier one. Repeat as necessary.
rungs separating you from the top of the ladder. So climb up one rung; this will reduce the instance at hand to an easier one. Repeat as necessary.
Example instance:
- You are 4 rungs away from the top of the ladder. The instance would become simpler if you were only 3 rungs away from the top, so climb up one rung.
- You are 3 rungs away from the top of the ladder. The instance would become simpler if you were only 2 rungs away from the top, so climb up one rung.
- You are 2 rungs away from the top of the ladder. The instance would become simpler if you were only 1 rung away from the top, so climb up one rung.
- You are 1 rung away from the top of the ladder. The instance would become simpler if you were only 0 rungs away from the top, so climb up one rung.
- You are at the top of the ladder. Congratulations! You've solved the problem.
- You are 1 rung away from the top of the ladder. The instance would become simpler if you were only 0 rungs away from the top, so climb up one rung.
- You are 2 rungs away from the top of the ladder. The instance would become simpler if you were only 1 rung away from the top, so climb up one rung.
- You are 3 rungs away from the top of the ladder. The instance would become simpler if you were only 2 rungs away from the top, so climb up one rung.
Problem: Differentiate a function with respect to  . The generic form of this problem is Differentiate with respect to
. The generic form of this problem is Differentiate with respect to  . The instance is the specific function you want to differentiate.
. The instance is the specific function you want to differentiate.
Solution: If the function to be differentiated is a power of  , a constant, or a standard function of
, a constant, or a standard function of  (for example,
(for example, 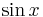 ), this is a trivial instance; you can simply use the power rule or look up the derivative in your calculus textbook. Otherwise, find the last step in computing the function; it may be addition, subtraction, multiplication, division, or a function application. Then use the sum rule, difference rule, product rule, quotient rule, or chain rule, as appropriate, on the subexpression(s), which is/are necessarily simpler than the original function. By applying these rules enough times, any elementary function can be differentiated.
), this is a trivial instance; you can simply use the power rule or look up the derivative in your calculus textbook. Otherwise, find the last step in computing the function; it may be addition, subtraction, multiplication, division, or a function application. Then use the sum rule, difference rule, product rule, quotient rule, or chain rule, as appropriate, on the subexpression(s), which is/are necessarily simpler than the original function. By applying these rules enough times, any elementary function can be differentiated.
Example instance:
- We wish to differentiate
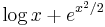 . This is a complex instance. The lowest-precedence operation is the addition, so we will use the sum rule; hence,
. This is a complex instance. The lowest-precedence operation is the addition, so we will use the sum rule; hence, 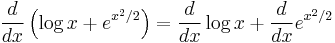 . Each of the two derivatives on the right side is a simpler instance of this problem.
. Each of the two derivatives on the right side is a simpler instance of this problem.
- We wish to differentiate
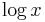 . This is a trivial instance, since the textbook will tell you that
. This is a trivial instance, since the textbook will tell you that 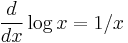 .
. - We wish to differentiate
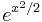 . The lowest-precedence operation is the exponential; it is done last. So we will use the chain rule, hence,
. The lowest-precedence operation is the exponential; it is done last. So we will use the chain rule, hence, 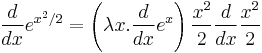 .
.
- We wish to differentiate
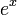 . This is a trivial instance; the textbook indicates that its derivative is
. This is a trivial instance; the textbook indicates that its derivative is 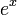 .
. - We wish to differentiate
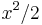 . This is a complex instance; we use the rule
. This is a complex instance; we use the rule 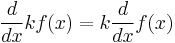 , where
, where  is a constant. Thus,
is a constant. Thus, 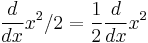 .
.
- We wish to differentiate
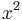 . This is a trivial instance; the power rule gives its derivative as
. This is a trivial instance; the power rule gives its derivative as 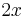 .
.
- We wish to differentiate
- Therefore, the derivative of
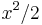 is
is 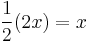 .
.
- We wish to differentiate
- Therefore, the derivative of
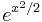 is
is 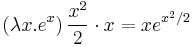 .
.
- We wish to differentiate
- Therefore, the derivative of
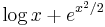 is
is 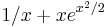 . Congratulations! You've solved the problem.
. Congratulations! You've solved the problem.
Problem: Obtain a certain item. The generic form of this problem is Obtain. The instance is the specific item you wish to obtain.
Solution: If you already have the item, then you don't need to do anything; this is a trivial instance. If the item is commercially available and you wouldn't mind buying it, then simply do so; this is also a trivial instance. Otherwise, build it yourself. Identify simpler components of which the item is composed. Obtaining these components comprises easier instances of the given problem. After obtaining the required components, assemble them into the item desired.
Example instance:
- You live on a farm and want to prepare a rack of ribs for dinner. This is a complex instance. To solve it, you will have to first obtain the ribs and the barbecue sauce.
- You wish to obtain a rack of ribs. This is a complex instance; you will need need to slaughter and butcher a pig.
- You wish to obtain a pig. You don't raise pigs on your farm, but your neighbour raises pigs. This is a trivial instance, as you can simply buy a pig from your neighbour.
- You have obtained a pig. Now slaughter and butcher it. You have obtained a rack of ribs.
- You wish to obtain barbecue sauce. Unfortunately, you don't have any left, and your neighbour doesn't either, and it's a holiday, so the market is closed. This is a complex instance. You look in your cookbook, and find a recipe for barbecue sauce consisting of ketchup, sugar, and vinegar. You will need to obtain these and mix them.
- You wish to obtain ketchup. You already have ketchup, so this is a trivial instance.
- You wish to obtain sugar. You already have sugar, so this is a trivial instance.
- You wish to obtain vinegar. You already have vinegar, so this is a trivial instance.
- Having obtained ketchup, sugar, and vinegar, you mix them in the correct ratios, thereby obtaining barbecue sauce.
- You wish to obtain a rack of ribs. This is a complex instance; you will need need to slaughter and butcher a pig.
- Having obtained ribs and barbecue sauce, you apply the sauce to the ribs, apply heat, and then apply more sauce. Congratulations! You have obtained a dish of ribs, ready to enjoy.
Examples from computer science
Problem: Given two non-negative integers  and
and  , find their greatest common divisor (GCD), denoted
, find their greatest common divisor (GCD), denoted 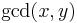 . The general form of the problem is compute the GCD. The specific instance is given by
. The general form of the problem is compute the GCD. The specific instance is given by  and
and  .
.
Solution: If 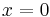 , we have a trivial case, and the answer is
, we have a trivial case, and the answer is  . If
. If 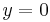 , again it is a trivial case, and the answer is
, again it is a trivial case, and the answer is  . Otherwise, we have a complex case. But if we can somehow make one of the numbers smaller, the problem will become simpler, and ultimately one of the two numbers will have to reach zero. It turns out that
. Otherwise, we have a complex case. But if we can somehow make one of the numbers smaller, the problem will become simpler, and ultimately one of the two numbers will have to reach zero. It turns out that 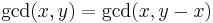 , if
, if 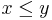 (and the reverse,
(and the reverse, 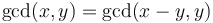 if
if 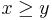 ). By reducing the problem to one of these two possible subproblems, and repeating enough times, we eventually discover the answer.
). By reducing the problem to one of these two possible subproblems, and repeating enough times, we eventually discover the answer.
Example instance:
- We wish to find the GCD of 30 and 48. Since neither is 0, this is a complex case. We note that
 .
.
- We wish to find the GCD of 30 and 18. Since neither is 0, this is a complex case. We note that
 .
.
- We wish to find the GCD of 12 and 18. Since neither is 0, this is a complex case. We note that
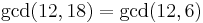 .
.
- We wish to find the GCD of 12 and 6. Since neither is 0, this is a complex case. We note that
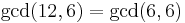 .
.
- We wish to find the GCD of 6 and 6. Since neither is 0, this is a complex case. We note that
 .
.
- We wish to find the GCD of 6 and 0. This is a trivial case, and the answer is 6.
- We wish to find the GCD of 6 and 6. Since neither is 0, this is a complex case. We note that
- We wish to find the GCD of 12 and 6. Since neither is 0, this is a complex case. We note that
- We wish to find the GCD of 12 and 18. Since neither is 0, this is a complex case. We note that
- We wish to find the GCD of 30 and 18. Since neither is 0, this is a complex case. We note that
Implementation (C):
int gcd(int x, int y) { if (x == 0) return y; else if (y == 0) return x; else if (x >= y) return gcd(x-y, y); else return gcd(x, y-x); }
Problem: Locate a file by name on a filesystem, or conclude that the file does not exist. The problem here is find if exists; the instance consists of the filename of the file we wish to find, and the directory that we wish to search.
Solution: If the directory is empty, this is a trivial instance, and we give up. Otherwise, we will have to examine the contents of the directory. For each entry of the directory, if it is a file, check whether it matches the given filename; if so, we are done. If not, go on to the next one. If the entry is a directory itself, this is a subinstance of the problem: attempt to locate the desired file in the subdirectory; again, if we succeed, then we are done, and otherwise, we must go on to the next entry.
Example instance:
- We wish to locate the file
apache2.confsomewhere under the root directory of a Unix-like system. The root directory is not empty; it contains the entries:bin/ dev/ etc/ home/ lib/ proc/ root/ tmp/ usr/ var/- We wish to locate the file
apache2.confsomewhere in/bin. This directory is not empty; it contains the entries:cat chgrp chmod chown cp date dd df echo... and no subdirectories. None of these matches the desired filename, so we give up. (This turned out to be a trivial instance, since this directory contains no subdirectories on which to recurse.) - We wish to locate the file
apache2.confsomewhere in/dev. This directory is not empty; it contains the entries:console full mem null port ptmx pts/ random sda sda1 stderr stdin stdout tty zero. We check each of these in turn: no, no, no, no, no, no... a directory. We have to searchpts/for the file.- We wish to locate the file
apache2.confsomewhere in/dev/pts. This directory is empty, so this is a trivial instance, and we give up.
- We wish to locate the file
- We continue trying to match against
randomand so on: no, no, no, no, no, no, no, no. We give up; the fileapache2.confis not in/dev. - We wish to locate the file
apache2.confsomewhere in/etc. This directory is not empty; it contains the entries:apache2/ crontab fstab group gshadow hostname hosts inittab localtime motd passwd profile resolv.conf shadow shells X11/.- We wish to locate the file
apache2.confsomewhere in/etc/apache2. This directory is not empty; it contains the entries:apache2.conf conf.d/ envvars httpd.conf magic mods-available/ mods-enabled/ ports.conf sites-available/ sites-enabled/. We find a match at the first entry; success!
- We wish to locate the file
- We wish to locate the file
Implementation (Python):
import os def find(path, name): for entry in os.listdir(path): # iterate through every entry newpath = os.path.join(path, entry) # get the absolute path to this entry if os.path.isdir(newpath) and not os.path.islink(newpath): # descend into directory print "Descending into directory " + newpath ret = find(newpath, name) # complex case; recurse into subproblem if ret: return ret else: # it's a file; just check whether it matches if entry == name: return newpath return False # give up res = find("/", "apache2.conf") if res: print "File found at " + res else: print "File not found"