Woburn Challenge 2015-16 Round 1 - Senior Division
Problem 4: Chocolate Milk

After the finals of the 2015-16 Woburn Challenge, young programmers from all over the region will be invited to Woburn for a top-secret after-party (not really though)! The school has generously agreed to nourish them with copious amounts of chocolate milk.
To this end, the Student Activity Council (SAC) has acquired N (2 ≤ N ≤ 200) cisterns with infinite capacities, and positioned them at distinct heights off the ground. The cisterns are uniquely numbered from 1 to N in order of their heights from lowest to highest. For each cistern i (such that 2 ≤ i ≤ N), there will be Pi (0 ≤ Pi ≤ 107) litres of chocolate milk pumped into it per second, directly from Scarborough's local chocolate milk farm. Additionally, there will be a pipe leading down from each cistern i to a different cistern Ci. According to the laws of gravity, chocolate milk can only flow from a higher cistern to a lower cistern, so it's guaranteed that i > Ci. The pipe coming out of i will be wide enough to allow at most Fi (1 ≤ Fi ≤ 107) litres of chocolate milk to flow through it per second. Chocolate milk flows through the system as one might expect – for every cistern, the amount of chocolate milk flowing out of it cannot exceed the total amount flowing into it (both directly from the farm and down from the other cisterns).
However, PEG has received enough funding this year to be able to upgrade K (0 ≤ K < N) of the N − 1 pipes. When a pipe is upgraded, it permanently becomes able to support an infinite amount of chocolate milk flowing through it.
Cistern 1 is located in Woburn's cafeteria, and the students will have permission to drink from it at will! Coding is a strenuous sport, so we know that everyone will be extremely thirsty. So the more chocolate milk flows into that cistern, the more they will collectively drink. And the more chocolate milk they consume, the more their coding skills will improve for next year's Challenge. Given the configuration of cisterns and pipes, and provided that we choose the optimal set of K pipes to upgrade, what's the maximum rate of incoming chocolate milk flow (in litres per second) that cistern 1 can attain?
In test cases worth 25% of the marks, K ≤ 2.
In a subset of those test cases worth 10% of the marks, K = 0.
Input Format
Line 1 of input will contain two space-separated integers N and K, respectively representing the number of cisterns and the number of upgrades allowed.
Line 2 to N of input will each contain information about a cistern. Specifically, line i of input (for i = 2..N) will contain three space-separated integers Pi, Ci, and Fi, respectively representing the rate at which chocolate milk is being pumped into cistern i (in litres per second), the cistern that the pipe from cistern i flows into, and the maximum rate at which chocolate milk (in litres per second) can flow through this pipe.
Output Format
Output a single integer, the maximum rate of incoming chocolate milk flow that cistern 1 can attain, in litres per second.
Sample Input
5 2 20 1 50 20 1 30 20 2 5 40 2 30
Sample Output
90
Explanation
There are 5 cisterns and we're allowed to upgrade 2 of the pipes. The network of cisterns and pipes is depicted in the following diagrams. The numbers on the pipes represent the maximum rates of chocolate milk flow, and the bottom numbers on the cisterns represent the rate at which chocolate milk is being pumped into them. The left diagram depicts the original configuration, and the right diagram depicts the system after pipes have been upgraded.
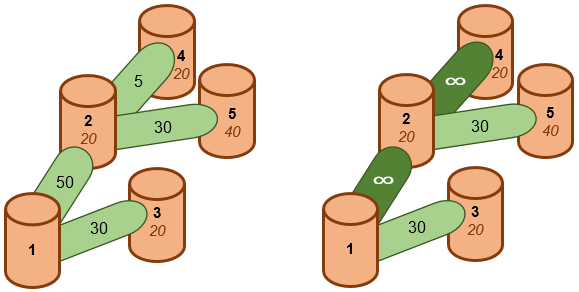
By upgrading the pipes flowing down from cisterns 2 and 4, cistern 1 in the cafeteria is able to receive 20 litres/second from cistern 3, 20 litres/second from cistern 2 directly, and 50 litres/second from cistern 2 indirectly (20 of which came from cistern 4 and 30 of which came from cistern 5). In total, this allows cistern 1 to receive 20 + 20 + 50 = 90 litres/second.
All Submissions
Best Solutions
Point Value: 20 (partial)
Time Limit: 3.00s
Memory Limit: 16M
Added: Oct 17, 2015
Author: SourSpinach
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)