Sane's Monthly Algorithms Challenge: November 2008
Infinite Degrees of Separation (Advanced Level)
The hypothesis known as the 6 Degrees of Separation suggests that everyone knows everyone else through an average chain of 6 people.But if we only consider chains linked together by best friends, then this hypothesis severely breaks down. In many cases, we even obtain “infinite degrees of separation”, when two people can not be linked together at all by such a chain.
We would like to demonstrate this on some sample data. Given a list of who considers whom to be their best friend, we would like to know for particular pairs of people, how many unique chains can be formed to join the two together (e.g. If the number of unique chains is zero, then there are infinite degrees of separation between the two people).
A link in a chain can either be a person and his/her best friend, or a best friend and the person who considers him/her to be their best friend. The uniqueness of a chain is determined by its set of links, and a valid chain can not use the same person more than once.
Input
The first line of the input consists of two integers,n (1 ≤ n ≤
100,000), and m (1 ≤ m ≤ 100,000), representing the number of people in
the sample data, and the number of query pairs, respectively.The next
n lines (line i : 0 ≤ i ≤ n-1) that follow will each contain a
single integer j ∈ [0, n-1] \ {i} (0 .. n-1, discluding i). This line
states that the i'th person considers the j'th person to be his or her
best friend.The next
m lines that follow will each contain two integers i and j (0
≤ i, j ≤ n-1, i ≠ j), representing a question about the number of
unique chains which exist between person i and person j.
Output
In m lines, respond to each question (in order) with an integer representing the number of unique chains which exist between the two people.Sample Input
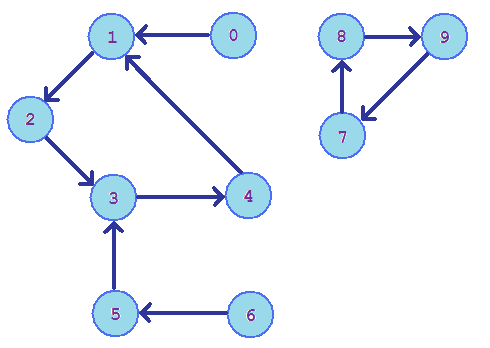
10 31
2
3
4
1
3
5
8
9
7
0 4
5 6
6 9
Sample Output
2
1
0
Diagram
All Submissions
Best Solutions
Point Value: 30 (partial)
Time Limit: 3.00s
Memory Limit: 64M
Added: Jan 15, 2009
Author: DrSane
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...