National Olympiad in Informatics, China, 1998
Day 2, Problem 3 - Parallel Computing
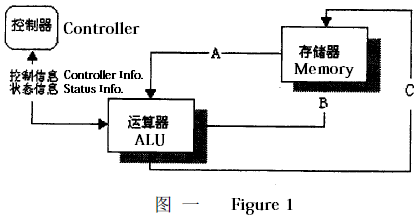
The arithmetic logic unit (ALU) is an important component in computers due to its function of performing mathematical calculations. Figure 1 is a simplified depiction of how an ALU operates. To perform one calculation, the controller instructs the ALU to accept two source operands A and B from the memory unit. After a certain amount of time, C, the resulting value of the computation, is sent back and written to a specified location in the memory unit.
The time it takes the ALU to perform a certain operation is given by the following table.
| Operation Type | Operation | Operation Time |
|---|---|---|
| 1 | C = A + B | Tadd |
| 2 | C = A − B | Tsub |
| 3 | C = A × B | Tmul |
| 4 | C = A ÷ B | Tdiv |
When evaluating complex mixed operation expressions, the ALU turns into a "bottleneck" of high-speed computing. To achieve faster computation results, computer scientists have designed a computer with two ALUs running in parallel. Its structure is depicted in figure 2.
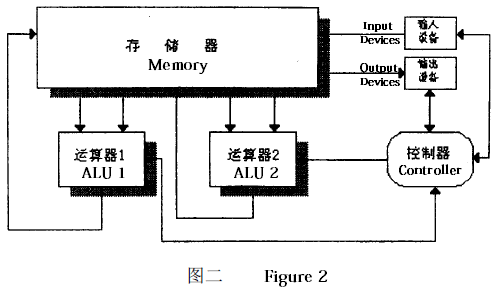
The ability for the two ALUs to perform calculations at the same time drastically improves the speed of the entire computer. The parallel computer has two types of commands:
The operation command: OP Time Alu_no Operate_no Address1 Address2 Address3
- The keyword
OPis followed by six parameters: Timeindicates the time that the command was issued.Alu_nois the ID of the ALU that should bear the operation (Alu_no∈ {1, 2}).Operate_nois the type of operation being performed (Operate_no∈ {1, 2, 3, 4}).Address1,Address2are the addresses of the two operands in the memory unit.Address3is the address in the memory unit at which the result of the operation should be stored.
The termination command: END Time Address
- The keyword
ENDis followed by two parameters: Timeis the time when the entire computation process should terminate.Addressis the address in memory at which the final computation result should be stored.
Each ALU can only process a single operation command at a time, and the termination command ends all computation.
You are to write a program for the controller that, given an expression to evaluate, directs the parallel computer depicted in figure 2 to compute the correct value for the expression while minimizing the total computation time.
Input Format
The first line of input consists of four positive integers, each no larger than 1000, the values of Tadd, Tsub, Tmul, and Tdiv. The second line of input contains the mixed-operation expression (no longer than 255 characters). Each variable in the expression will consist of a single uppercase alphabetical letter. The initial values for the variables will be stored in consecutive memory addresses 1, 2, … according to alphabetical order (e.g. if the expression only uses the variables A, B, and D, then address 1 will initially store the value of A, 2 will store B, and 3 will store D).
Output Format
The output should contain the optimal commands for evaluating the expression, in order of when they are issued (commands issued at the same time can be given in any order), one command per line.
Guarantees
The initial time when the controller process may start is 0.
Time values in this problem will all be in the same unit.
There are at most 1000 available addresses in the memory unit (at locations 1 through 1000).
The time for reading from and writing to the memory unit is negligible.
If both ALUs simultaneously try to operate on the memory unit, then ALU 1 always operates before ALU 2.
Sample Input
2 2 4 12 C+(A+B)*C-E/F+F
Sample Output
OP 0 1 1 1 2 6 OP 0 2 4 4 5 8 OP 2 1 1 3 5 7 OP 4 1 3 6 3 10 OP 8 1 1 10 7 11 OP 12 1 2 11 8 12 END 14 12
All Submissions
Best Solutions
Point Value: 25 (partial)
Time Limit: 1.00s
Memory Limit: 16M
Added: May 01, 2014
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...