National Olympiad in Informatics, China, 2014
Day 1, Problem 3 - Deletion Game
Recently, little Z has been addicted to a new type of deletion game. This game takes place on an n×m grid. Initially, the grid cells are filled with integers from 0 to 9. Through deletion, the cells become blank (denoted by −1). We will denote the cell at row i, column j as Ai,j, and let its coordinates be (i, j).
Given three parameters lmin, lmax, and K, the player can make no greater than K moves. For each move, the player must first find a path of length l in the grid. Formally, this path is represented by two length l sequences x1, x2, …, xl and y1, y2, …, yl that satisfy the following conditions:
- 1 ≤ xi ≤ n and 1 ≤ yi ≤ m, where 1 ≤ i ≤ l, meaning that (xi, yi) is a valid cell on the grid.
- |xi − xi+1| + |yi − yi+1| = 1 where 1 ≤ i < l, meaning that (xi, yi) and (xi+1, yi+1) are two neighbouring cells on the grid.
- xi ≠ xj or yi ≠ yj, where 1 ≤ i < j ≤ l, meaning that the path does not repeat cells.
- Axi, yi ≠ −1, where 1 ≤ i ≤ l, meaning that the path does not go through any blank cells.
- Ax1, y1 ≠ 0, meaning that the path does not start with the number 0.
- lmin ≤ l ≤ lmax, meaning that the length of the path has to fall within the given range.
Then, the player will string the digits on the path together into an integer N. Formally:
The game will provide two parameters c1 and c2 to calculate the player's score on a move:
- If N is a prime number, then the prime subscore is lc1, otherwise the prime subscore is 1.
- If N is a palindromic number (i.e. when viewed as a string, N is identical whether its letters are arranged forwards or reverse), then the palindromic subscore is lc2, otherwise the palindromic subscore is 1.
- If the prime subscore and the palindromic subscore are both equal to 1, then then overall score for the move is 0. Otherwise, the overall score for the move is equal to the sum of the prime subscore and the palindromic subscore.
If after a move the move's overall score is 0, then you will have wasted the move and the game's state will not change. Otherwise if the move's overall score is greater than 0, then all cells on the path will be set to blank, and the cells above the blank will drop down. Formally, the following operations take place:
- Set Axi, yi ← −1, where 1 ≤ i ≤ l.
- Examine every cell in the grid. If a cell (i, j) satisfies i ≠ n, Ai,j ≠ −1, and Ai+1,j = −1, then set Ai+1,j ← Ai,j and Ai,j ← −1. Repeat this step until no more cells in the grid satisfy the conditions.
The following is an example of a player making a move and deleting some cells. In this case, n = m = 3 and c1 = c2 = 1. The player starts off facing the board in figure 1.
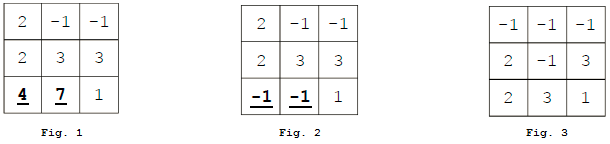
- The player selects the path containing digits 4 and 7, which strung together makes N = 47. Since 47 is a prime number, the prime subscore is lc1 = 21 = 2. Since 47 is not a palindromic number, the palindromic subscore is 1. Thus, the overall score for the move is 2 + 1 = 3.
- Since the score of the move is nonzero, the path's values are deleted (as in figure 2).
- Digits above the blank cells drop down (as in figure 3). At this point, the player is ready to make the next move.
We will also give you a parameter F. After the player has made every move, the player's final score will be determined using F. If F = 0, then the player's final score is equal to the sum of the scores across every move. If F = 1, then the player's final score will be sum of the scores across every move, divided by 2d, rounded down. Formally:
where d is the final number of non-blank cells at the end of the game.
Little Z finds himself hooked to this game, unable to step away. She would like your help. For the given parameters, provide a series of moves to play the game. Of course, the final score should be as high as possible.
Input Format
There will be 10 files game1.in ~ game10.in that will be given to your program (through standard input). They can be downloaded here for you to study: game.zip.
For each test case:
The first line of input contains an integer from 1 to 10, representing the test case number. Test case gamei.in will have i on its first line.
The second line of input will contain eight space-separated integers n, m, K, lmin, lmax, c1, c2, and F.
The next n lines will each contain m integers, representing the array A. Adjacent integers on the same line will be separated by a space.
The input will not contain any extra or trailing spaces.
Output Format
The first line of output should contain a single integer M (0 ≤ M ≤ K), representing the number of moves you would like to make.
M lines should follow, each describing one move. For each of these lines, the first integer should be l, representing the length of the path. 2l integers should follow on the same line. They are, respectively, x1, y1, x2, y2, …, xl, yl.
The output should not contain extra spaces or lines. Adjacent values on the same line should be separated by a single space.
Your output should not exceed 1MB in size. The data guarantees that a valid answer will not exceed this upper bound.
Sample Input 1
0 3 3 100 2 3 1 1 0 2 1 1 2 3 3 4 7 1
Sample Output 1
4 2 2 2 3 2 2 3 1 3 2 2 2 1 3 1 3 1 3 2 3 3 3
Explanation 1
Four deletions are made. The deleted paths and move scores are, respectively: 37 (for a score of 2 + 1 = 3), 41 (for a score of 2 + 1 = 3), 22 (for a score of 1 + 2 = 3), and 131 (for a score of 3 + 3 = 6). Since F = 0, the final score is simply 15. There may exist a more optimal solution.
Sample Input 2
0 1 3 100 2 3 1 1 1 2 1 1
Sample Output 2
1 2 1 2 1 3
Explanation 2
Only one deletion is made. The deleted path is 11. The score is 2 + 2 = 4. Since F = 1, the final score is equal to 4, the sum of scores across all moves, divided by 21 = 2, rounded down, which is 2. If the deleted path was 211, then an optimal final score of 4 would have been obtained.
Grading
For each test case, we have set up 9 parameters a10, a9, …, a2. If your output is invalid, then your score will be 0 for the test case. Otherwise, assuming your final score is wuser, then your score out of 10 for the test case will be given by the following table.
| Score | Condition |
|---|---|
| 10 | wuser ≥ a10 |
| 9 | wuser ≥ a9 |
| 8 | wuser ≥ a8 |
| 7 | wuser ≥ a7 |
| 6 | wuser ≥ a6 |
| 5 | wuser ≥ a5 |
| 4 | wuser ≥ a4 |
| 3 | wuser ≥ a3 |
| 2 | wuser ≥ a2 |
| 1 | wuser > 0 |
Experimentation
We provide a tool game_check (GNU/Linux: game_check, Windows: game_check.exe) for you to help check if your output program is valid. The usage for this program (on Windows) is:
game_check.exe <case_no>
where <case_no> is the number of the test case. For example:
game_check.exe 3
will test game3.out to determine whether it is accepted.
After you invoke this program, the checker will provide the result to the execution of your output file in one of the following ways:
- Abnormal termination: An unknown error occurred.
Input/Output file does not exist.: We cannot load your input or output file.Output invalid!: There is an error with your output file. A general error message may now be included.Details: xxx.: Other information.Correct! Your answer is x.: Your output is acceptable. Your final score is x.
Note from admin: Please ensure that both the input file gameX.in and output file gameX.out are present and correctly formatted when you run the program. Note that the first integer in the input file is the test case number T, and will be ignored. Furthermore, this program is only guaranteed to work on the dataset provided in the zip file above. Running the program on your own input is not guaranteed to yield the correct results. If for whatever reason you are having trouble running the checker programs on your platform, please post a comment letting us know of the problem.
All Submissions
Best Solutions
Point Value: 30 (partial)
Time Limit: 10.00s
Memory Limit: 512M
Added: May 19, 2015
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...