PEG Judge - NOI '09 - Pipe Marbles

National Olympiad in Informatics, China, 2009

Day 2, Problem 2 - Pipe Marbles

Pipe Marbles is one of little X's favorite games. In this question, we shall consider a simple version of it. A screen of the game is depicted below in figure 1.

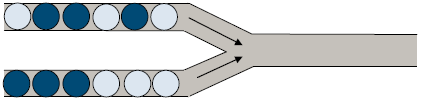
(Figure 1.)

At the start of the game, the upper and lower pipes on the left side each contain a fixed amount of marbles (some are dark colored and some are light colored), and the output pipe on the right side is empty. In each move, one can select a pipe from the left side and move the rightmost marble from that pipe to the right output pipe.

For instance, we can move a marble from the lower left pipe into the output pipe, as depicted below in figure 2.

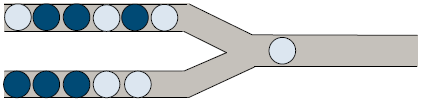
(Figure 2.)

Assuming there are n marbles in the upper and m marbles in the lower pipe, then completing the game will require n + m moves to move all of the marbles from the left pipe to the output pipe. At the end, the n + m marbles in the output pipe from left to right will form an output sequence.

As a math fanatic, little X knows that he has a total of C(n + m, n) different ways to complete the game, where different ways can produce the same output sequence. For example, consider the game scenario depicted below in figure 3:

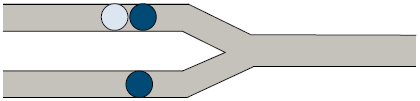
(Figure 3.)

We let the letter A represent light colored balls and the letter B represent dark colored balls. Denote the action of moving a ball from the upper pipe to the right pipe as U, and the action of moving a ball from the lower pipe to the right pipe as D, then there are a total of C(2+1, 1) = 3 different ways to complete the game. Respectively, they are UUD, UDU, and DUU. Finally, the corresponding output sequences produced are (from left to right) respectively BAB, BBA, and BBA. The latter two ways therefore produce the same output sequence.

Assuming that it's possible to create K different types of final output sequences, and that there are a_i ways (i.e. the number of different sequence of moves) to create the i-th type of these output sequences. Little X has known for a long time that:

$\displaystyle \sum_{i=1}^{k}a_i = C(n+m,n)$

Thus, little X wishes to compute the value of:

$\displaystyle \sum_{i=1}^{k}a_i^2$

Can you help him determine this value? Since it may be very large, you are only required to output it modulo 1024523 (the remainder when divided by 1024523).

Note: The aforementioned C(n + m, n) represents a combination. C(a, b) equals the number of ways to choose b items from a collection of a different items.

Input Format

The first line contains two integers n and m, respectively representing the number of marbles in the upper and lower pipes on the left side.
The second line contains a string of A's and B's of length n, describing the marbles in the upper left side pipe from left to right. A represents a light colored marble and B represents a dark colored marble.
The third line contains a string of A's and B's of length m, describing the marbles in the lower left side pipe.

Output Format

The output should consist of a single line with a single integer, $\textstyle \sum_{i=1}^{k} a_i^{2}$ modulo 1024523.

Sample Input

2 1
AB
B

Sample Output

Explanation

The sample follows the example in figure 3, where there are two possible distinct output sequences. The sequence BAB has 1 way of being created, and the sequence BBA has 2 ways of being created. Therefore, the answer is 5.