National Olympiad in Informatics, China, 2008
Day 2, Problem 2 - Candy Rain
There is a beautiful fairy tale: Once upon a time in a far away land by the edge of the world, there existed a "Candy Kingdom". This nation is filled with skyscrapers; meanwhile, the little trails, flowers, and grass are all made out of candy. What's more magical is that the sky is filled with rainbow colored candy clouds floating about. Very often, heavy candy rain will pour onto the ground. The red colors are strawberry candy, the yellow colors are lemon, the green colors are mint, the black colors are chocolate, and so on. The children of Candy Kingdom will frequently hold open pouches of all sizes to catch the candy pieces that fall from the sky, bringing them home for their friends to enjoy.
Having a very big sweet tooth, little Z longs to be able to visit this fairy tale kingdom. As the old saying goes, what you think about in the day, you will dream about during the night. So one night, little Z dreamed that he has arrived in Candy Kingdom. He discovered that at any given moment, all of the clouds in the sky will have different colors. These different colored clouds continuously drop candies of corresponding colors. What's even more interesting is that all of the clouds are in constant back and forth motion. There's no harm in imagining that there are borders to the sky, which is why the clouds just happen to be moving back and forth between the two borders of the sky. During each unit of time, a cloud moves one unit of distance either to the left or to the right. When a cloud hits the left border of the sky, it will change its direction and start moving to the right; when a cloud completely moves past the right border of the sky, it will change its direction and start moving to the left.
We may as well think of the sky as a Cartesian coordinate plane, where clouds are represented by line segments (which may degenerate to points):
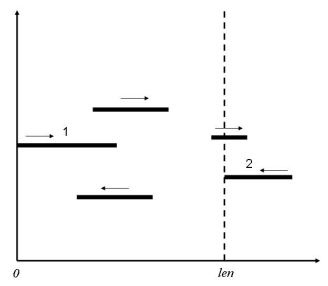
In the figure above, we set the left border of the sky to be 0 and the right border to be len. The figure contains a total of 5 clouds. The cloud labeled 1 is just changing its direction to move rightwards. The cloud labeled 2 is just changing its direction to move leftwards. The vertical coordinates of the clouds may be ignored, for the clouds will never affect each other during their movement process.
Little Z noticed that new clouds will continuously form in the sky (during some time, at some starting position, moving in some direction), and some clouds after moving for a certain time will disappear from the sky. While clouds are in motion, candy will continuously fall from them. Little Z decided to bring many bags to catch the falling candy. Bags have unlimited capacities, but the size of their openings are limited. For example at time T, little Z carries a bag which has an opening spanning the horizontal range [L, R]. If [L, R] contains a position x where candy falls, then the bag will be able to catch the candy. In extreme cases, the range of the bag's opening can be a point such as [0, 0] or [1, 1], but the bag will still be able to catch candy at the corresponding positions. It is generally known that the amount of candy one can catch is rather larger, so little Z would like to know for each time (the moment he pulls out a bag) how many different colors of candy can his bag catch? The falling times of the candy are negligible.
Input Format
The first line contains two positive integers n and len, representing the total number of events and the sky's "boundary", respectively.
For the following n lines, each line describes one event. All events happen in the input order. The first number of each line k (k = 1, 2, or 3) specifies the type of event that happens. There are three types of events: Insert, Query, and Delete. Their formats are as follows:
| Event Type | Input Format | Explanation |
|---|---|---|
Insert(A new cloud appears in the sky) |
1 Ti Ci Li Ri Di |
At time Ti, a new cloud of color Ci spanning the range [Li, Ri] will appear in the sky. The initial direction of the cloud may be leftwards (Di = −1) or rightwards (Di = 1). These parameters will satisfy 0 ≤ Li ≤ Ri ≤ len, and Di ∈ {−1, 1}. The data guarantees that at any given moment, the sky will not contain two clouds that are the same color. |
Query(Determine how many different colors of candy a bag can catch) |
2 Ti Li Ri |
At time Ti, little Z uses a bag with an opening that spans the range [Li, Ri] to catch candy. He would like to know how many different colors of them he can catch. The parameters will satisfy 0 ≤ Li ≤ Ri ≤ len. |
Delete(A cloud disappears from the sky) |
3 Ti Ci |
At time Ti, the cloud colored Ci will disappear from the sky. The data guarantees that the sky will contain a cloud with color Ci at that time. |
Output Format
For each Query event, output one line containing one integer – the number of different colors of candy that can be caught by the corresponding bag.
Sample Input
10 10 1 0 10 1 3 -1 2 1 0 0 2 11 0 10 2 11 0 9 1 11 13 4 7 1 2 13 9 9 2 13 10 10 3 100 13 3 1999999999 10 1 2000000000 10 0 1 1
Sample Output
1 1 0 2 1
Explanation
There are 10 total events, including 3 Insert events, 5 Query events, and 2 Delete events.
At time 0, a cloud of color 10 appears in the sky, initially spanning the range [1, 3] and moving left.
At time 1, a bag with the range [0, 0] can catch candy of color 10 (with the cloud at [0, 2]).
At time 11, a bag with the range [0, 10] can catch candy of color 10 (with the cloud at [10, 12]).
At time 11, a bag with the range [0, 9] cannot catch any candy of color 10 (with the cloud at [10, 12]).
At time 11, a cloud of color 13 appears in the sky, initially spanning the range [4, 7] and moving right.
At time 13, a bag with the range [9, 9] can catch candy of color 10 (with the cloud at [8, 10]) and candy of color 13 (with the cloud at [6, 9]) for 2 different colors.
At time 13, a bag with the range [10, 10] can only catch candy of color 10 (with the cloud at [8, 10]), but cannot catch any candy of color 13 (with the cloud at [6, 9]).
At time 100, the cloud of color 13 disappears from the sky.
At time 1999999999, the cloud of color 10 disappears from the sky.
At time 2000000000, another cloud of color 10 appears in the sky, initially spanning the range [0, 1] and moving right.
Constraints
All of the data will satisfy 0 ≤ Ti ≤ 2000000000 and 1 ≤ Ci ≤ 1000000.
The data guarantees that { Ti } forms a non-decreasing sequence T1 ≤ T2 ≤ … ≤ Tn−1 ≤ Tn.
For all of the Insert events, let Pi = Ri − Li, representing the length of each cloud.
| Test Case | n | len | Pi |
|---|---|---|---|
| 1 | 20 | 10 | ≤ len |
| 2 | 200 | 100 | ≤ len |
| 3 | 2000 | 1000 | ≤ len |
| 4 | 100000 | 10 | ≤ len |
| 5 | 100000 | 100 | ≤ 2 |
| 6 | 150000 | 1000 | ≤ 3 |
| 7 | 200000 | 1000 | ≤ 3 |
| 8 | 100000 | 1000 | ≤ len |
| 9 | 150000 | 1000 | ≤ len |
| 10 | 200000 | 1000 | ≤ len |
All Submissions
Best Solutions
Point Value: 30 (partial)
Time Limit: 2.00s
Memory Limit: 128M
Added: Aug 01, 2014
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...