National Olympiad in Informatics, China, 2007
Day 1, Problem 1 - Social Network
In the study of social networks, we commonly use graph theory to explain certain social phenomena.
Let's look at a problem regarding this. There are n people in a social group. Between people, there are different levels of relationships. We represent this relationship network using an undirected graph with n nodes. If two different people are familiar with each other, then there will exist an undirected edge between their corresponding nodes on the graph. Additionally, the edge will have a positive weight c – the smaller the value of c, the closer the relationship between the two people.
We can use the shortest path between the corresponding nodes of two people s and t to measure the closeness of their relationship. Note that other nodes on the shortest path provides some level of benefit to the relationship between s and t, and that these nodes have a certain level of importance with respect to s and t's relationship. Through analysis of the shortest paths passing through node v, we can measure v's importance level to the entire social network.
Observing that there may be multiple shortest paths between nodes A and B, we revise our definition of the importance level as follows:
Let Cs,t represent the number of shortest paths between nodes s and t, and Cs,t (v) represent the number of shortest paths between nodes s and t which passes through v. The importance level of node v to the social network is defined as:
To ensure that I(v) and Cs,t (v) are always defined, we will only deal with social networks that can be represented by connected, undirected graphs. Furthermore, there will always exist a shortest path of finite length between any pair of nodes.
Given such a weighted, undirected graph representing the social network, please calculate the importance level of each node.
Input Format
The first line of input contains two integers n and m, representing the number of nodes and the number of undirected edges in the social network. The nodes in the graph are numbered consecutively from 1 to n.
For the next m lines, each line contains three integers a, b, and c describing an undirected edge connecting nodes a and b with weight c. Note that there will be at most one undirected edge between any pair of nodes, and no loops will occur within the graph (where the two ends of an edge rest on the same node).
Output Format
Output n lines, each line containing a single real number, accurate to 3 digits after the decimal point. Line i represents the importance of node i to the social network. Your outputted numbers will be considered correct if the absolute differences between them and the correct values do not exceed 0.001.
Sample Input
4 4 1 2 1 2 3 1 3 4 1 4 1 1
Sample Output
1.000 1.000 1.000 1.000
Explanation
The social network is depicted in the following figure.
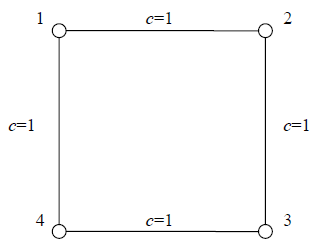
Regarding node 1, only the shortest path from 2 to 4 and the shortest path from 4 to 2 pass through it. There are 2 different shortest paths between nodes 2 and 4. According to the definition, the importance level of node 1 is 1/2 + 1/2 = 1. Due to the symmetry of the graph, the other three edges also have importance levels of 1.
Constraints
For 50% of the test cases: n ≤ 10, m ≤ 45
For 100% of the test cases: n ≤ 100, m ≤ 4500, and the weight c of any edge will be a positive integer satisfying 1 ≤ c ≤ 1000.
It is guaranteed that the data will consist of connected, undirected graphs, and that the number of shortest paths between any two nodes will not exceed 1010.
All Submissions
Best Solutions
Point Value: 15 (partial)
Time Limit: 1.00s
Memory Limit: 256M
Added: Jul 24, 2014
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...