2015 Mock CCC by Alex and Timothy

Problem S5: Kongou

You are the admiral of an admirable fleet of battleships! Your flagship is the Kongou*, and you have never lost a single battle in your entire career. This is because you have adopted the foolproof strategy of blocking off all critical rivers before engaging in battle.

The battlefield can be thought of as N (1 ≤ N ≤ 100 000) seas connected to each other by bidirectional rivers, each joining a pair of seas. No sea will be directly connected to itself by a river, but the same pair of seas can be connected by multiple rivers, and it may not be possible to draw the rivers on a map without some of them crossing each other. A river is considered critical if after blocking it, the pair of seas originally joined by it are no longer reachable from each other. Specifically, you can reach a sea v from another sea u if there exists a sequence of seas S₁, S₂, …, S_n where n > 1, S₁ = u, S_n = v, and S_i is connected to S_{i + 1} for 1 ≤ i < n.

You and your fleet girls are immortal, and so you get called upon to fight every few years, for a total of T (1 ≤ T ≤ 200 000) times. The passage of time is not kind to the battlefield, and so the rivers that connect the seas change often (the seas themselves remain the same though). Normally, this would make it hard to quickly devise a plan for each battle, but there is still hope. In your experience, you have observed that there are M (1 ≤ M ≤ 100 000) basic formations. A formation is simply a set of rivers, and each battlefield you fight on can be represented by combining two formations (see the sample input for a better understanding).

For each battlefield, you would like to determine the number of critical rivers.

*Kongou, based off of the Kongō.

Input Format

The first line of input will contain the integers N, M, and T, each separated by a single space.

The second line of input will have T + 1 numbers, A₀, A₁, …, A_T (1 ≤ A_i ≤ M). The i-th time you fight will be represented by the combination of formations A_i−1 and A_i (for 1 ≤ i ≤ T).

The next M lines will contain descriptions of a single formation. Formation i (1 ≤ i ≤ M) on line i + 2 will be described with 2K_i + 1 (1 ≤ K_i ≤ 200 000) integers in this order: K_i x_i,1 y_i,1 … x_i,Ki y_i,Ki. For all 1 ≤ j ≤ K_i, there is a river between lakes x_i,j and y_i,j in formation i (where x_i,j ≠ y_i,j and 1 ≤ x_i,j, y_i,j ≤ N).

It is guaranteed that the sum of all K_i will not exceed 200 000.

Output Format

The output shoud consist of T lines. Line i should have the number of critical rivers on the battlefield you fight on for the i−th time (1 ≤ i ≤ T).

Scoring

For test cases worth at least 30% of the points, the additional constraints N, M, K_i, T ≤ 2000 will hold.

Sample Input 1

4 3 4
1 1 2 3 1
1 1 2
1 3 4
2 2 3 2 3

Sample Output 1

0
2
1
1

Sample Input 2

7 3 3
1 2 3 1
4 1 2 1 3 5 7 6 7
4 2 3 3 4 4 5 5 6
3 1 4 4 7 2 6

Sample Output 2

2
2
2

Explanation for Sample 2

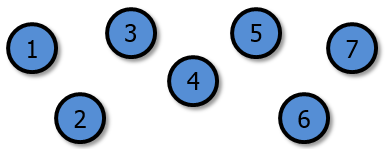
Originally, there are 7 seas numbered from 1 to 7.
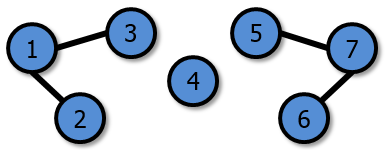
The first formation looks like this:	The second formation looks like this:
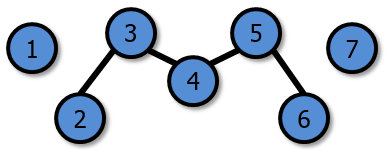
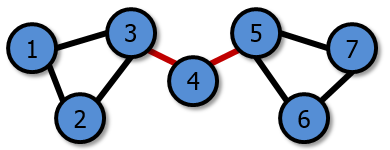
The third formation looks like this:	In the first battle, the battlefield is made up of the first and second formations and looks like this: The two critical rivers (in red) are 3 ↔ 4 and 4 ↔ 5.
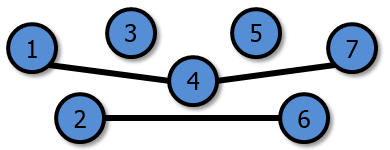
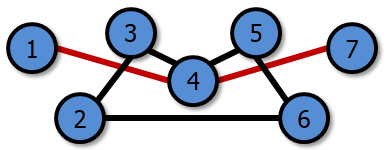
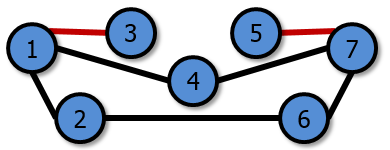
In the second battle, the battlefield is made up of the second and third formations and looks like this: The two critical rivers (in red) are 1 ↔ 4 and 4 ↔ 7.	In the third and final battle, the battlefield is made up of the third and first formations and looks like this: The two critical rivers (in red) are 1 ↔ 3 and 5 ↔ 7.

All Submissions
Best Solutions

Point Value: 40 (partial)
Time Limit: 20.00s
Memory Limit: 256M
Added: Feb 18, 2015
Authors: FatalEagle, Alex

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)

It's quiet in here...