IOI '95 - Eindhoven, Netherlands
Shopping Offers
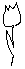 = 2,
= 2,
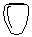 = 5,
= 5,
 +
+
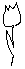 +
+
 = 5,
= 5,
 +
+
 +
+
 = 10,
= 10,
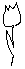 +
+
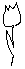 +
+
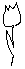 +
+
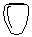 +
+
 = ?
= ?
In a shop each kind of product has a price. For example, the price of a flower is 2 ICU (Informatics Currency Units) and the price of a vase is 5 ICU. In order to attract more customers, the shop introduces some special offers.
A special offer consists of one or more product items for a reduced price. Examples:
- three flowers for 5 ICU instead of 6, or
- two vases together with one flower for 10 ICU instead of 12.
Write a program that calculates the price a customer has to pay for certain items, making optimal use of the special offers. That is, the price should be as low as possible. You are not allowed to add items, even if that would lower the price.
For the prices and offers given above, the (lowest) price for three flowers and two vases is 14 ICU: two vases and one flower for the reduced price of 10 ICU and two flowers for the regular price of 4 ICU.
Input Format
The input has a set of offers followed by a purchase.
| Line 1: | s, the number of special offers, (0 ≤ s ≤ 99). |
| Line 2..s+1: | Each line describes an offer using several integers. The first integer is n (1 ≤ n ≤ 5), the number of products that are offered. The subsequent n pairs of integers c and k indicate that k items (1 ≤ k ≤ 5) with product code c (1 ≤ c ≤ 999) are part of the offer. The last number p on the line stands for the reduced price (1 ≤ p ≤ 9999). The reduced price of an offer is less than the sum of the regular prices. |
| Line s+2: | The first line contains the number b (0 ≤ b ≤ 5) of different kinds of products to be purchased. |
| Line s+3..s+b+2: | Each of the subsequent b lines contains three values: c, k, and p. The value c is the (unique) product code (1 ≤ c ≤ 999). The value k indicates how many items of this product are to be purchased (1 ≤ k ≤ 5). The value p is the regular price per item (1 ≤ p ≤ 999). At most 5×5 = 25 items can be in the basket. |
Output Format
A single line with one integer: the lowest possible price to be paid for the purchases.
Sample Input
2 1 7 3 5 2 7 1 8 2 10 2 7 3 2 8 2 5
Sample Output
14
All Submissions
Best Solutions
Point Value: 15 (partial)
Time Limit: 2.00s
Memory Limit: 8M
Added: Dec 25, 2013
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...