PEG Judge - IOI '95 - Packing Rectangles

IOI '95 - Eindhoven, Netherlands

Packing Rectangles

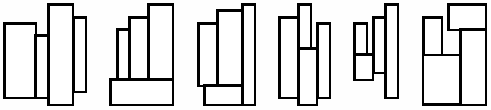
Figure 1: The six basic layouts of four rectangles

Four rectangles are given. Find the smallest enclosing (new) rectangle into which these four may be fitted without overlapping. By smallest rectangle, we mean the one with the smallest area.

All four rectangles should have their sides parallel to the corresponding sides of the enclosing rectangle. Figure 1 shows six ways to fit four rectangles together. These six are the only possible basic layouts, since any other layout can be obtained from a basic layout by rotation or reflection. Rectangles may be rotated 90 degrees during packing.

There may exist several different enclosing rectangles fulfilling the requirements, all with the same area. You must produce all such enclosing rectangles.

Input Format

Four lines, each containing two positive space-separated integers that represent the lengths of a rectangle's two sides. Each side of a rectangle is at least 1 and at most 50.

Output Format

The output contains one line more than the number of solutions. The first line contains a single integer: the minimum area of the enclosing rectangles. Each of the following lines contains one solution described by two numbers p and q with p ≤ q. These lines must be sorted in ascending order of p, and must all be different.