IOI '95 - Eindhoven, Netherlands

Bar Codes

A bar-code symbol consists of alternating dark and light bars, starting with a dark bar on the left. Each bar is a number of units wide. Figure 1 shows a bar-code symbol consisting of 4 bars that extend over 1 + 2 + 3 + 1 = 7 units.

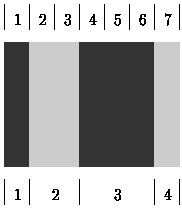
Figure 1: Four fences and some of their letter strings (joints not to scale)

In general, the bar code BC(n, k, m) is the set of all symbols with k bars that together extend over exactly n units, each bar being at most m units wide. For instance, the symbol in Figure 1 belongs to BC(7, 4, 3) but not to BC(7, 4, 2).

0: 1000100  |  8: 1100100
1: 1000110  |  9: 1100110
2: 1001000  | 10: 1101000
3: 1001100  | 11: 1101100
4: 1001110  | 12: 1101110
5: 1011000  | 13: 1110010
6: 1011100  | 14: 1110100
7: 1100010  | 15: 1110110

Figure 2: All symbols of BC(7, 4, 3)

Figure 2 shows all 16 symbols in BC(7, 4, 3). Each `1' represents a dark unit, each `0' a light unit. The symbols appear in lexicographic (dictionary) order. The number on the left of the colon (`:') is the rank of the symbol. The symbol in Figure 1 has rank 4 in BC(7, 4, 3).

Input Format

The first line of input contains the numbers n, k, and m (1 ≤ n, k, m ≤ 33). On the second line is a number s (0 ≤ s ≤ 100). The following s lines each contain some symbol in BC(n, k, m), represented by `0's and `1's as in Figure 2.

Output Format

On the first line of output your program should write the total number of symbols in BC(n, k, m) (Subtask A). On each of the s following lines, it should write the rank of the corresponding symbol in the input (Subtask B).

Sample Input

7 4 3
5
1001110
1110110
1001100
1001110
1000100

Sample Output

16
4
15
3
4
0

All Submissions
Best Solutions

Point Value: 20 (partial)
Time Limit: 2.00s
Memory Limit: 8M
Added: Apr 13, 2014

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)