IOI '14 - Taipei, Taiwan
Wall
Jian-Jia is building a wall by stacking bricks of the same size ogether. This wall consists of n columns of bricks, which are numbered 0 to n − 1 from left to right. The columns may have different heights. The height of a column is the number of bricks in it.
Jian-Jia builds the wall as follows. Initially there are no bricks in any column. Then, Jian-Jia goes through k phases of adding or removing bricks. The building process completes when all k phases are finished. In each phase Jian-Jia is given a range of consecutive brick columns and a height h, and he does the following procedure:
- In an adding phase, Jian-Jia adds bricks to those columns in the given range that have less than h bricks, so that they have exactly h bricks. He does nothing on the columns having h or more bricks.
- In a removing phase, Jian-Jia removes bricks from those columns in the given range that have more than h bricks, so that they have exactly h bricks. He does nothing on the columns having h bricks or less.
Your task is to determine the final shape of the wall.
Example
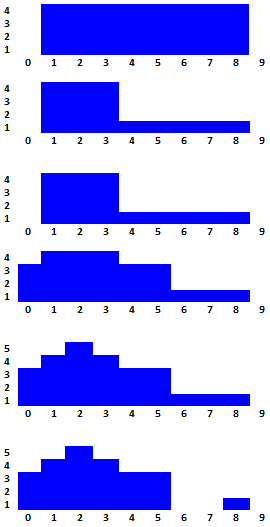
We assume that there are 10 brick columns and 6 wall building phases. All ranges in the following table are inclusive. Diagrams of the wall after each phase are shown below.
| phase | type | range | height |
|---|---|---|---|
| 0 | add | columns 1 to 8 | 4 |
| 1 | remove | columns 4 to 9 | 1 |
| 2 | remove | columns 3 to 6 | 5 |
| 3 | add | columns 0 to 5 | 3 |
| 4 | add | column 2 | 5 |
| 5 | remove | columns 6 to 7 | 0 |
Since all columns are initially empty, after phase 0 each of the columns 1 to 8 will have 4 bricks. Columns 0 and 9 remain empty. In phase 1, the bricks are removed from columns 4 to 8 until each of them has 1 brick, and column 9 remains empty. Columns 0 to 3, which are out of the given range, remain unchanged. Phase 2 makes no change since columns 3 to 6 do not have more than 5 bricks. After phase 3 the numbers of bricks in columns 0, 4, and 5 increase to 3. There are 5 bricks in column 2 after phase 4. Phase 5 removes all bricks from columns 6 and 7.
Given the description of the k phases, please calculate the number of bricks in each column after all phases are finished.
Input Format
Line 1 of input consists of the two integers n, and k. n is the number of columns of the wall, and k is the number of phases.
Line 2 + i of input each consists of the format: op[i], left[i], right[i], and height[i].
op[i]is the type of phase i: 1 for an adding phase and 2 for a removing phase, for 0 ≤ i ≤ k − 1.- the range of columns in phase i starts with column
left[i]and ends with columnright[i](including both endpointsleft[i]andright[i]), for 0 ≤ i ≤ k − 1. You will always haveleft[i]≤right[i]. height[i]is the height parameter of phase i, for 0 ≤ i ≤ k − 1.
Output Format
The output should consist of n integers, one per line, describing the result. Line i should describe the final number of bricks in column i, for 0 ≤ i ≤ n − 1.
Sample Input 1
10 3 1 3 4 91220 1 5 9 48623 2 3 5 39412
Sample Output 1
0 0 0 39412 39412 39412 48623 48623 48623 48623
Sample Input 2
10 6 1 1 8 4 2 4 9 1 2 3 6 5 1 0 5 3 1 2 2 5 2 6 7 0
Sample Output 2
3 4 5 4 3 3 0 0 1 0
Subtasks
For all subtasks the height parameters of all phases are nonnegative integers less than or equal to 100,000.
| subtask | % of points | n | k | note |
|---|---|---|---|---|
| 1 | 8 | 1 ≤ n ≤ 10,000 | 1 ≤ k ≤ 5,000 | no additional limits |
| 2 | 24 | 1 ≤ n ≤ 100,000 | 1 ≤ k ≤ 500,000 | all adding phases are before all removing phases |
| 3 | 29 | 1 ≤ n ≤ 100,000 | 1 ≤ k ≤ 500,000 | no additional limits |
| 4 | 39 | 1 ≤ n ≤ 2,000,000 | 1 ≤ k ≤ 500,000 | no additional limits |
All Submissions
Best Solutions
Point Value: 25 (partial)
Time Limit: 3.00s
Memory Limit: 256M
Added: Jul 29, 2014
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...