IOI '14 - Taipei, Taiwan
Tile
Place tiles on the floor
We have a 2n by 2n floor with 4n unit squares. Each square can be identified by its x and y coordinates (both from 0 to 2n − 1). We want to cover this floor with four types of 2 by 2 L-shaped tiles, as shown in the following figure. The tiles cannot overlap, and they can only be placed on grid boundary. In addition, there is exactly a square that we cannot cover with tiles. Please find a way to cover the entire floor with tiles.
Example
In the following example we have n = 3 and 64 squares. The blue square at (1, 6) cannot be covered by any tile. This figure shows a possible way to cover the floor. To identify a tile we will use the x and y coordinates. For example, the green tile in the figure can be identified by (6, 2), (7, 2), and (7, 3).
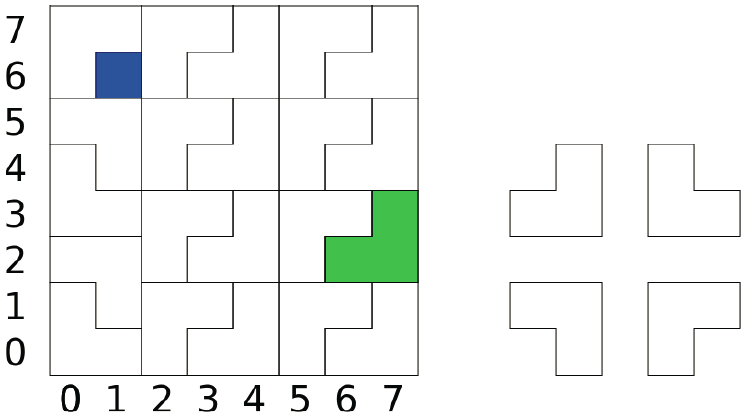
Statement
Write a program to cover the floor with tiles.
Input Format
The input consists of one line with 3 integers n, x, and y. n indicates that the size of the floor is 2n by 2n. x and y are the coordinates of the square that cannot be covered with tiles.
Output Format
The output should consist of a list of tile positions. Each line of the output should contain six space-separated integers x1, y1, x2, y2, x3, and y3 to describe the position of one tile. For example, if we want to place the green tile as the first tile, we can output the integers 6, 2, 7, 2, 7, and 3. The three squares of a tile can appear in any order, so we can also set them as 7, 2, 7, 3, 6, and 2. The tiles can also appear in any order.
Sample Input 1
1 0 0
Sample Output 1
0 1 1 0 1 1
Sample Input 2
1 1 0
Sample Output 2
0 0 0 1 1 1
Subtask 1 [5% of points]
- n is 1.
Subtask 2 [15% of points]
- 1 ≤ n ≤ 2.
Subtask 3 [20% of points]
- 1 ≤ n ≤ 8, and x = y = 0.
Subtask 4 [60% of points]
- 1 ≤ n ≤ 8.
All Submissions
Best Solutions
Point Value: 15 (partial)
Time Limit: 2.00s
Memory Limit: 64M
Added: Jun 25, 2014
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)