IOI '13 - Brisbane, Australia
Wombats
The city of Brisbane has been taken over by large mutated wombats, and you must lead the people to safety.
The roads in Brisbane are laid out in a large grid. There are R horizontal roads that run east-to-west, numbered 0, …, (R - 1) in order from north to south, and C vertical roads that run north-to-south, numbered 0, …, (C - 1) in order from west to east, as shown in the picture below.
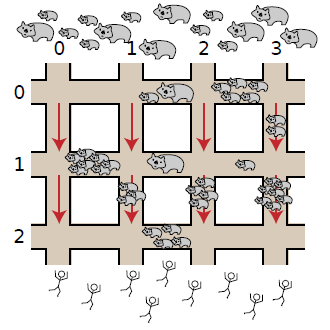
The wombats have invaded from the north, and the people are escaping to the south. People can run along horizontal roads in either direction, but on vertical roads they will only run towards the south, towards safety.
The intersection of horizontal road P with vertical road Q is denoted (P, Q). Each segment of road between two intersections contains some number of wombats, and these numbers may change over time. Your task is to guide each person from some given intersection in the north (on horizontal road 0) to some given intersection in the south (on horizontal road R - 1), taking them on a route that passes as few wombats as possible.
To begin, you will be given the size of the grid and the number of wombats on each road segment. Following this you will be given a series of E events, each of which is either:
- a change, which alters the number of wombats on some road segment; or
- an escape, where some person arrives at a given intersection on horizontal road 0, and you must find a route to a given intersection on horizontal road R - 1 that passes the fewest possible wombats.
You must handle these events by implementing the changeH, changeV and escape operations, as described below.
Examples
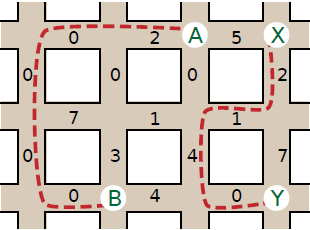
The picture above shows an initial map with R = 3 horizontal roads and C = 4 vertical roads, with the number of wombats marked on each segment. Consider the following series of events:
- A person arrives at intersection A = (0, 2) and wishes to escape to intersection B = (2, 1). The smallest number of wombats she can pass is 2, as indicated by a dashed line.
- Another person arrives at intersection X = (0, 3) and wishes to escape to intersection Y = (2, 3). The smallest number of wombats he can pass is 7, again indicated by a dashed line.
- Two change events occur: the number of wombats on the top segment of vertical road 0 changes to 5, and the number of wombats on the middle segment of horizontal road 1 changes to 6. See the circled numbers in the picture below.
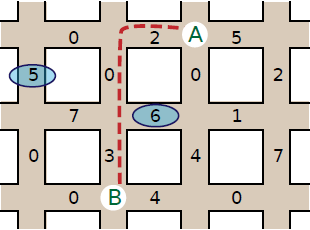
- A third person arrives at intersection A = (0, 2) and wishes to escape to intersection B = (2, 1). Now the smallest number of wombats she can pass is 5, as indicated by the new dashed line.
You will first be given the initial layout of the map, allowing you to initialise any variables and data structures.
Parameters:
- R: The number of horizontal roads.
- C: The number of vertical roads.
- H: A two-dimensional array of size R × (C - 1), where H[P][Q] gives the number of wombats on the segment of horizontal road between intersections (P, Q) and (P, Q + 1).
Your task is to implement the changeH, changeV and escape operations, as follows:
changeH: This operation will be called in the input when the number of wombats changes on the horizontal road segment between intersections (P, Q) and (P, Q + 1).
Parameters:
- P: Indicates which horizontal road is affected (0 ≤ P ≤ R - 1).
- Q: Indicates between which two vertical roads the segment lies (0 ≤ Q ≤ C - 2).
- W: The new number of wombats on this road segment (0 ≤ W ≤ 1,000).
changeV: This operation will be called when the number of wombats changes on the vertical road segment between intersections (P, Q) and (P + 1, Q).
Parameters:
- P: Indicates between which two horizontal roads the segment lies (0 ≤ P ≤ R - 2).
- Q: Indicates which vertical road is affected (0 ≤ Q ≤ C - 1).
- W: The new number of wombats on this road segment (0 ≤ W ≤ 1,000).
escape: This operation should calculate the fewest possible wombats a person must pass when
travelling from intersection (0, V1) to (R-1, V2).
Parameters:
- V1: Indicates where the person begins on horizontal row 0 (0 ≤ V1 ≤ C - 1).
- V2: Indicates where the person ends on horizontal row R - 1 (0 ≤ V2 ≤ C - 1).
Input Format
- line 1: R C
- line 2: H[0][0] … H[0][C-2]
- …
- lines (R + 1): H[R1][0] … H[R-1][C-2]
- lines (R + 2): V[0][0] … V[0][C-1]
- …
- line (2R): V[R-2][0] … V[R-2][C-1]
- next line: E
- next E lines: one event per line, in the order in which events occur
If C = 1, the empty lines containing the number of wombats on horizontal roads (lines 2 through R + 1) are not necessary.
The line for each event must be in one of the following formats:
- to indicate
changeH:1 P Q W - to indicate
changeV:2 P Q W - to indicate
escape:3 V1 V2
Output Format
For every call of escape, output an integer on a single line - the smallest number of wombats the person must pass.
Sample Case and Description
The following case describes the example above:
| Input | Description | Output |
|---|---|---|
3 4 0 2 5 7 1 1 0 4 0 0 0 0 2 0 3 4 7 | R = 3, C = 4 | |
5 | E = 5 | |
3 2 1 | escape 2 1 | 2 |
3 3 3 | escape 3 3 | 7 |
2 0 0 5 | changeV 0 0 5 | |
1 1 1 6 | changeH 1 1 6 | |
3 2 1 | escape 2 1 | 5 |
Constraints
- 2 ≤ R ≤ 5,000
- 1 ≤ C ≤ 200
- At most 500 changes (operations of either
changeHorchangeV) - At most 200,000
escapeoperations - At most 1,000 wombats on any segment at any time
Subtasks
| Subtask | Percent of Points | Additional Input Constraints |
|---|---|---|
| 1 | 9 | C = 1 |
| 2 | 12 | R, C ≤ 20, and there will be no changeH or changeV operations |
| 3 | 16 | R, C ≤ 100, and there will be at most 100 escape operations |
| 4 | 18 | C = 2 |
| 5 | 21 | C ≤ 100 |
| 6 | 24 | (None) |
All Submissions
Best Solutions
Point Value: 40 (partial)
Time Limit: 22.00s
Memory Limit: 256M
Added: Jul 18, 2013
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)