IOI '12 - Sirmione/Montichiari, Italy
Ideal City
Leonardo, like many other Italian scientists and artists of his age, was extremely interested in city planning and urban design. He aimed to model an ideal city: comfortable, spacious and rational in its usage of resources, far away from the narrow, claustrophobic cities of the Middle Ages.
The Ideal City
The city is made of N blocks placed on an infinite grid of cells. Each cell is identified by a pair of coordinates (row, column). Given a cell (i, j), the adjacent cells are: (i - 1, j), (i + 1, j), (i, j - 1), and (i, j + 1). Each block, when placed onto the grid, covers exactly one of the cells. A block can be placed onto the cell (i, j) if and only if 1 ≤ i, j ≤ 231 - 2. We will use the coordinates of the cells to also refer to the blocks on top of them. Two blocks are adjacent if they are placed in adjacent cells. In an ideal city, all of its blocks are connected in such a way that there are no "holes" inside its border, that is, the cells must satisfy both conditions below.
- For any two empty cells, there exists at least one sequence of adjacent empty cells connecting them.
- For any two non-empty cells, there exists at least one sequence of adjacent non-empty cells connecting them.
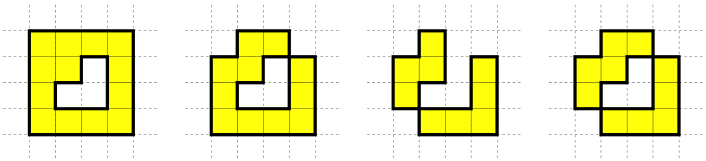
Example 1
None of the configurations of blocks below represent an ideal city: the first two on the left do not satisfy the first condition, the third one does not satisfy the second condition, and the fourth one does not satisfy either of the conditions.
Distance
When traversing the city, a hop indicates going from one block to an adjacent one. Empty cells cannot be traversed. Let v0, v1, …, vN-1 be the coordinates of the N blocks placed on the grid. For any two distinct blocks at coordinates vi and vj, their distance d(vi, vj) is the smallest number of hops that are required to go from one of these blocks to the other one.
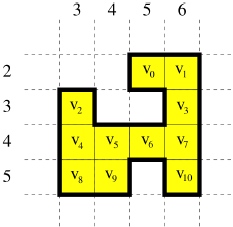
Example 2
The configuration below represents an ideal city made of N = 11 blocks at coordinates v0 = (2, 5), v1 = (2, 6), v2 = (3, 3), v3 = (3, 6), v4 = (4, 3), v5 = (4, 4), v6 = (4, 5), v7 = (4, 6), v8 = (5, 3), v9 = (5, 4), and v10 = (5, 6). For example, d(v1, v3) = 1, d(v1, v8) = 6, d(v6, v10) = 2, and d(v9, v10) = 4.
Statement
Your task is to, given an ideal city, write a program to compute the sum of all pairwise distances between blocks vi and vj for which i < j. Formally, your program should compute the value of the following sum:
Specifically, you have to write a program that, given N and two arrays X and Y that describe the city, calculates the formula above. Both X and Y are of size N; block i is at coordinates (X[i], Y[i]) for 0 ≤ i ≤ N - 1, and 1 ≤ X[i], Y[i] ≤ 231 - 2. Since the result may be too big to be represented using 32 bits, you should report it modulo 1 000 000 000 (one billion).
In Example 2, there are 11 × 10 / 2 = 55 pairs of blocks. The sum of all the pairwise distances is 174.
Input Format
Your program must read the input in the following format:
- line 1: N;
- lines 2, …, N + 1: X[i], Y[i].
Sample Input
11 2 5 2 6 3 3 3 6 4 3 4 4 4 5 4 6 5 3 5 4 5 6
Sample Output
174
Subtask 1 [11% of points]
You may assume that N ≤ 200.
Subtask 2 [21% of points]
You may assume that N ≤ 2 000.
Subtask 3 [23% of points]
You may assume that N ≤ 100 000.
Additionally, the following two conditions hold: given any two non-empty cells i and j such that X[i] = X[j], every cell between them is non-empty too; given any two non-empty cells i and j such that Y[i] = Y[j], every cell between them is non-empty too.
Subtask 4 [45% of points]
You may assume that N ≤ 100 000.
All Submissions
Best Solutions
Point Value: 25 (partial)
Time Limit: 1.00s
Memory Limit: 256M
Added: Aug 13, 2013
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...