IOI '08 - Cairo, Egypt

Pyramid Base

You have been asked to find the largest affordable location for constructing a new pyramid. In order to help you decide, you have been provided with a survey of the available land which has been conveniently divided into an M by N grid of square cells. The base of the pyramid must be a square with sides parallel to those of the grid.

The survey has identified a set of P possibly overlapping obstacles, which are described as rectangles in the grid with sides parallel to those of the grid. In order to build the pyramid, all the cells covered by its base must be cleared of any obstacles. Removing the ith obstacle has a cost Ci. Whenever an obstacle is removed, it must be removed completely, that is, you cannot remove only part of an obstacle. Also, please note that removing an obstacle does not affect any other obstacles that overlap it.

Task

Write a program that, given the dimensions M and N of the survey, the description of the P obstacles, the cost of removing each of the obstacles, and the budget B you have, finds the maximum possible side length of the base of the pyramid such that the total cost of removing obstacles does not exceed B.

Constraints and Grading

Your program will be graded on three disjoint sets of tests. For all of them, the following constraints apply:

1 ≤ M, N ≤ 1,000,000The dimensions of the grid.
1 ≤ Ci ≤ 7,000The cost of removing the ith obstacle.
1 ≤ Xi1 ≤ Xi2 ≤ MX coordinates of the leftmost and the rightmost cells of the ith obstacle.
1 ≤ Yi1 ≤ Yi2 ≤ NY coordinates of the bottommost and the topmost cells of the ith obstacle.

In the first set of tests worth 35% of points:

B = 0The budget you have. (You cannot remove any obstacles.)
1 ≤ P ≤ 1,000The number of obstacles in the grid.

In the second set of tests worth 35% of points:

0 ≤ B ≤ 2,000,000,000The budget you have.
1 ≤ P ≤ 30,000The number of obstacles in the grid.

In the third set of tests worth 30% of points:

B = 0The budget you have. (You cannot remove any obstacles.)
1 ≤ P ≤ 400,000The number of obstacles in the grid.

Input

Your program must read from the standard input the following data:

  • Line 1 contains two integers separated by a single space that represent M and N respectively.
  • Line 2 contains the integer B, the maximum cost you can afford (i.e., your budget).
  • Line 3 contains the integer P, the number of obstacles found in the survey.
  • Each of the next P lines describes an obstacle. The ith of these lines describes the ith obstacle. Each line consists of 5 integers: Xi1, Yi1, Xi2, Yi2, and Ci separated by single spaces. They represent respectively the coordinates of the bottommost leftmost cell of the obstacle, the coordinates of the topmost rightmost cell of the obstacle, and the cost of removing the obstacle. The bottommost leftmost cell on the grid has coordinates (1, 1) and the topmost rightmost cell has coordinates (M, N).

Output

Your program must write to the standard output a single line containing one integer, the maximum possible side length of the base of the pyramid that can be prepared. If it is not possible to build any pyramid, your program should output the number 0.

Example

Sample Input 1Sample Output 1
6 9
42
5
4 1 6 3 12
3 6 5 6 9
1 3 3 8 24
3 8 6 9 21
5 1 6 2 20
4

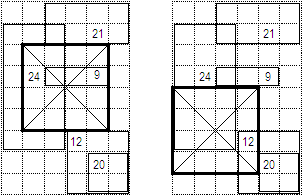
The figure shows two possible locations for the pyramid's base, both having a side of length 4.

Sample Input 2Sample Output 2
13 5
0
8
8 4 10 4 1
4 3 4 4 1
10 2 12 2 2
8 2 8 4 3
2 4 6 4 5
10 3 10 4 8
12 3 12 4 13
2 2 4 2 21
3

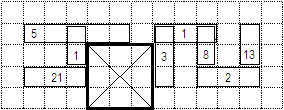
The figure shows the only possible location for the pyramid's base having a side of length 3.

All Submissions
Best Solutions


Point Value: 40 (partial)
Time Limit: 5.00s
Memory Limit: 256M
Added: Sep 03, 2013

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)

mohamed_essam on Jun 18, 2014 - 6:39:53 am UTC 35+35+35=100 !
  • (0/0)
each one of the three subtasks is 35% of the total score ?! O.o

Alex on Jun 18, 2014 - 7:18:50 pm UTC Re: 35+35+35=100 !
  • (0/0)
That was a copy-paste error, it's fixed now.