IOI '07 - Zagreb, Croatia
Pairs
Mirko and Slavko are playing with toy animals. First, they choose one of three boards given in the figure below. Each board consists of cells (shown as circles in the figure) arranged into a one, two or three dimensional grid.
 Board 1 |
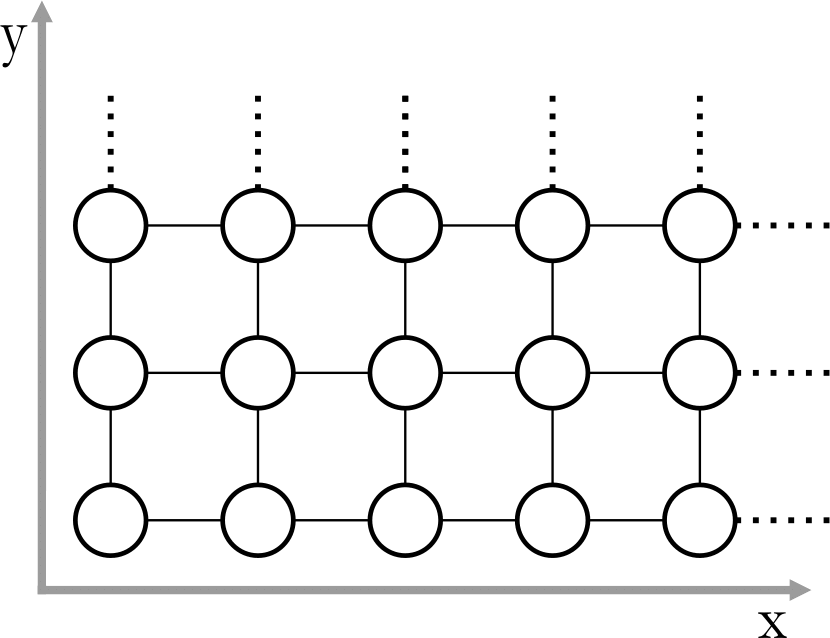 Board 2 |
 Board 3 |
Mirko then places N little toy animals into the cells.
The distance between two cells is the smallest number of moves that an animal would need in order to reach one cell from the other. In one move, the animal may step into one of the adjacent cells (connected by line segments in the figure).
Two animals can hear each other if the distance between their cells is at most D. Slavko's task is to calculate how many pairs of animals there are such that one animal can hear the other.
Write a program that, given the board type, the locations of all animals, and the number D, finds the desired number of pairs.
Input
The first line of input contains four integers in this order:
- The board type B (1 ≤ B ≤ 3);
- The number of animals N (1 ≤ N ≤ 100 000);
- The largest distance D at which two animals can hear each other (1 ≤ D ≤ 100 000 000);
- The size of the board M (the largest coordinate allowed to appear in the input):
- When B=1, M will be at most 75 000 000.
- When B=2, M will be at most 75 000.
- When B=3, M will be at most 75.
Each of the following N lines contains B integers separated by single spaces, the coordinates of one toy animal. Each coordinate will be between 1 and M (inclusive).
More than one animal may occupy the same cell.
Output
Output should consist of a single integer, the number of pairs of animals that can hear each other.
Note: use a 64-bit integer type to calculate and output the result (long long in C/C++, int64 in Pascal).
Sample Data
Input1 6 5 100 25 50 50 10 20 23 Output4 |
Input2 5 4 10 5 2 7 2 8 4 6 5 4 4 Output8 |
Input3 8 10 20 10 10 10 10 10 20 10 20 10 10 20 20 20 10 10 20 10 20 20 20 10 20 20 20 Output12 |
Clarification for the leftmost example. Suppose the animals are numbered 1 through 6 in the order in which they are given. The four pairs are:
- 1-5 (distance 5)
- 1-6 (distance 2)
- 2-3 (distance 0)
- 5-6 (distance 3)
Clarification for the middle example. The eight pairs are:
- 1-2 (distance 2)
- 1-4 (distance 4)
- 1-5 (distance 3)
- 2-3 (distance 3)
- 2-4 (distance 4)
- 3-4 (distance 3)
- 3-5 (distance 4)
- 4-5 (distance 3)
Note: In test cases worth a total of 30% of points, the number of animals N will be at most 1 000.
Furthermore, for each of the three board types, a solution that correctly solves all test cases of that type will be awarded at least 30% of points.
All Submissions
Best Solutions
Point Value: 30 (partial)
Time Limit: 4.00s
Memory Limit: 150M
Added: Sep 10, 2009
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...