IOI '07 - Zagreb, Croatia
Flood
In 1964 a catastrophic flood struck the city of Zagreb. Many buildings were completely destroyed when the water struck their walls. In this task, you are given a simplified model of the city before the flood and you should determine which of the walls are left intact after the flood.
The model consists of N points in the coordinate plane and W walls. Each wall connects a pair of points and does not go through any other points. The model has the following additional properties:
- No two walls intersect or overlap, but they may touch at endpoints;
- Each wall is parallel to either the horizontal or the vertical coordinate axis.
Initially, the entire coordinate plane is dry. At time zero, water instantly floods the exterior (the space not bounded by walls). After exactly one hour, every wall with water on one side and air on the other breaks under the pressure of water. Water then floods the new area not bounded by any standing walls. Now, there may be new walls having water on one side and air on the other. After another hour, these walls also break down and water floods further. This procedure repeats until water has flooded the entire area.
An example of the process is shown in the following figure.
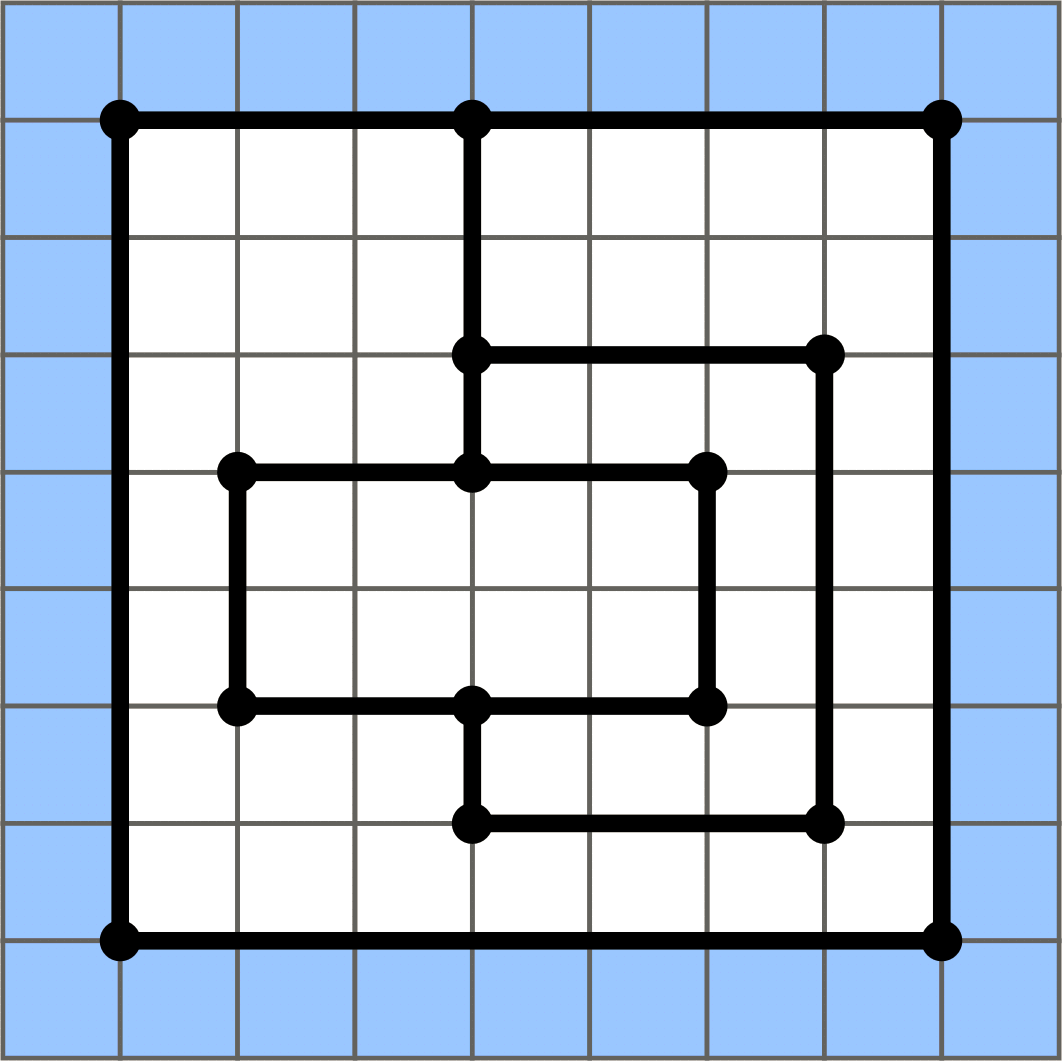 The state at time zero. Shaded cells represent the flooded area, while white cells represent dry area (air). |
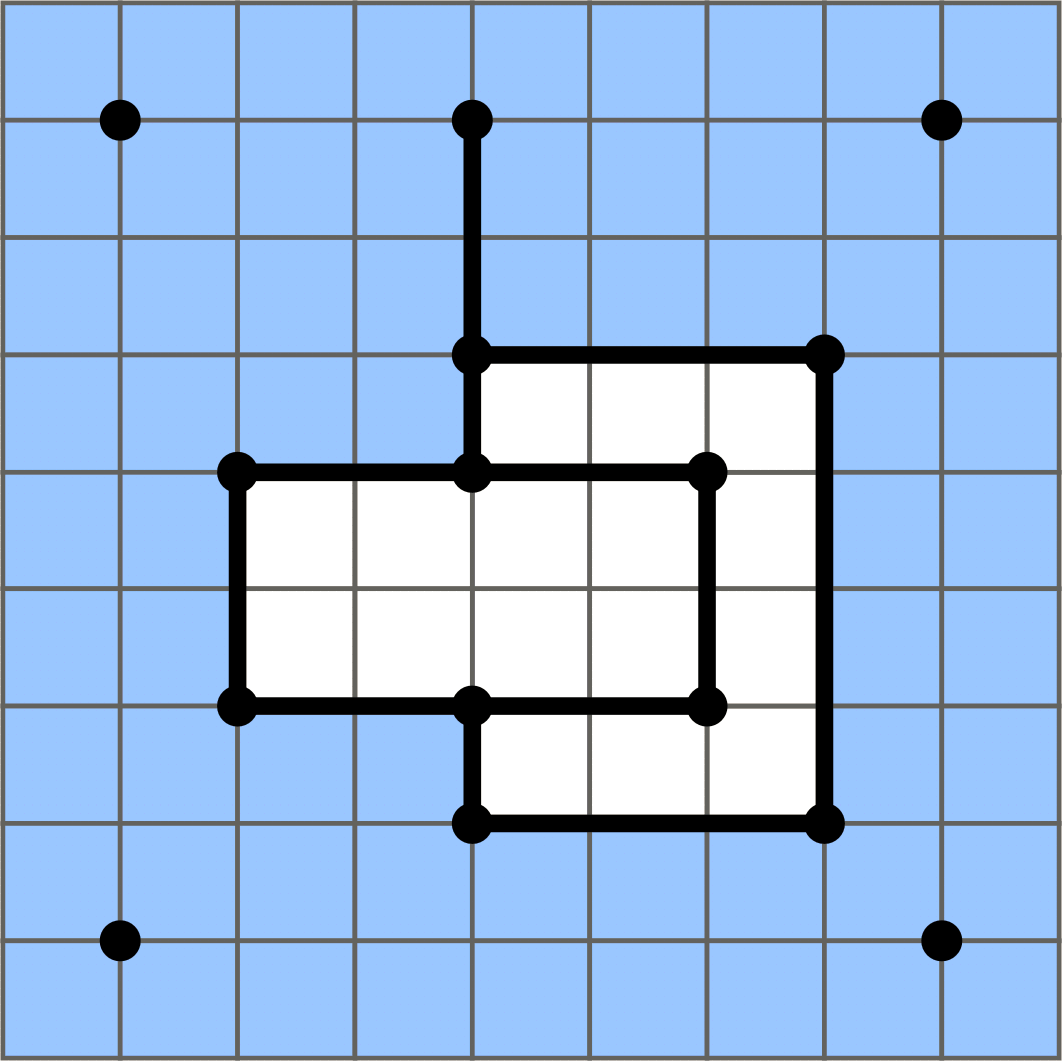 The state after one hour. |
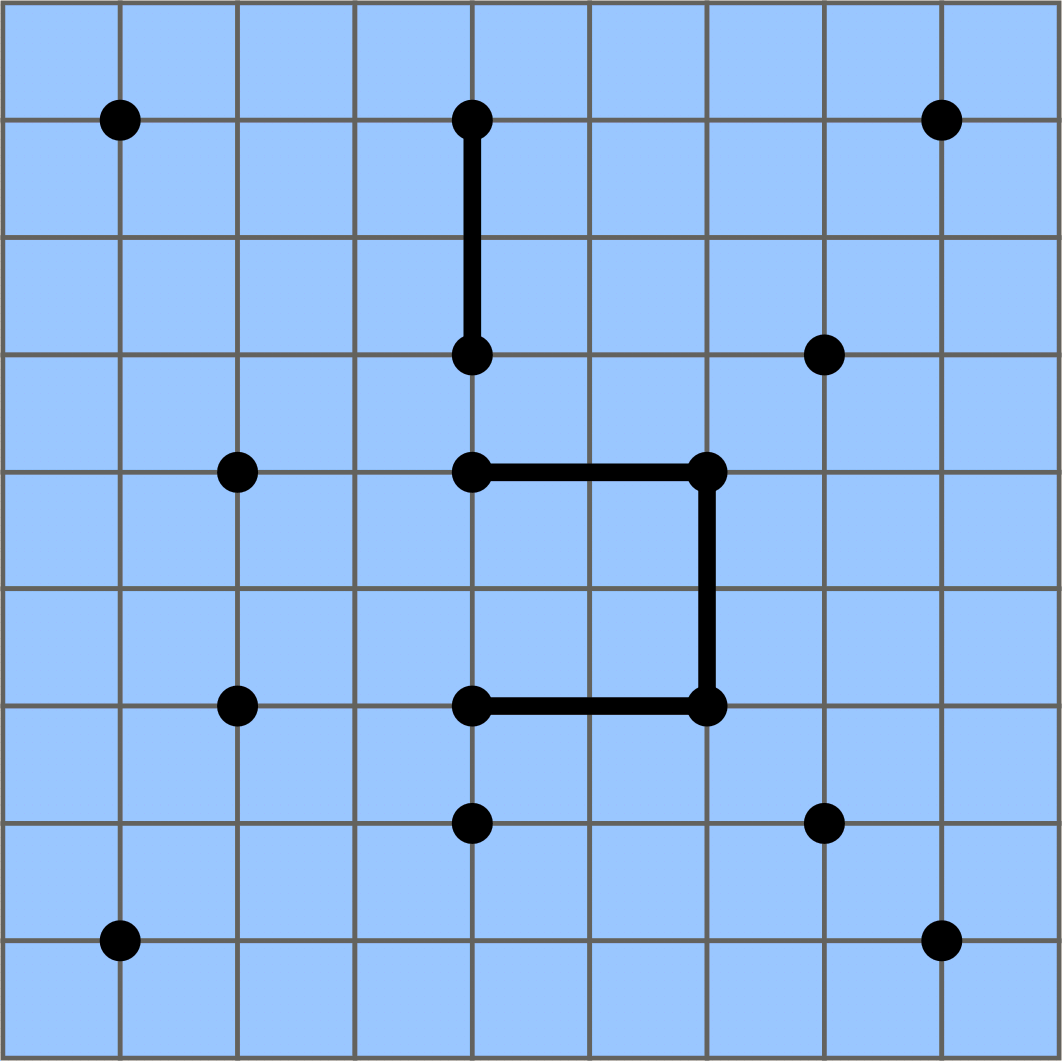 The state after two hours. Water has flooded the entire area and the 4 remaining walls cannot be broken down. |
Write a program that, given the coordinates of the N points, and the descriptions of W walls connecting these points, determines which of the walls are left standing after the flood.
Input
The first line of input contains an integer N (2 ≤ N ≤ 100 000), the number of points in the plane.
Each of the following N lines contains two integers X and Y (both between 0 and 1 000 000, inclusive), the coordinates of one point. The points are numbered 1 to N in the order in which they are given. No two points will be located at the same coordinates.
The following line contains an integer W (1 ≤ W ≤ 2N), the number of walls.
Each of the following W lines contains two different integers A and B (1 ≤ A ≤ N, 1 ≤ B ≤ N), meaning that, before the flood, there was a wall connecting points A and B. The walls are numbered 1 to W in the order in which they are given.
Output
The first line of output should contain a single integer K, the number of walls left standing after the flood.
The following K lines should contain the indices of the walls that are still standing, one wall per line. The indices may be output in any order.
Sample Input
15 1 1 8 1 4 2 7 2 2 3 4 3 6 3 2 5 4 5 6 5 4 6 7 6 1 8 4 8 8 8 17 1 2 2 15 15 14 14 13 13 1 14 11 11 12 12 4 4 3 3 6 6 5 5 8 8 9 9 11 9 10 10 7 7 6
Sample Output
4 6 15 16 17
This example corresponds to the figure above.
Note on test cases:
In test cases worth a total of 40% of the points, all coordinates will be at most 500.
In those same cases, and cases worth another 15% of the points, the number of points will be at most 500.
All Submissions
Best Solutions
Point Value: 30 (partial)
Time Limit: 2.00s
Memory Limit: 32M
Added: Sep 08, 2009
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
It's quiet in here...