IOI '05 - Nowy Sacz, Poland
Garden
Byteman owns the most beautiful garden in Bytetown. He planted n roses in his garden. Summer has come and the flowers have grown big and beautiful. Byteman has realized that he is not able to take care of all the roses on his own. He has decided to employ two gardeners to help him. He wants to select two rectangular areas, so that each of the gardeners will take care of the roses inside one area. The areas should be disjoint and each should contain exactly k roses.
Byteman wants to make a fence surrounding the rectangular areas, but he is short of money, so he wants to use as little fence as possible. Your task is to help Byteman select the two rectangular areas.
The garden forms a rectangle l meters long and w meters wide. It is divided into l·w squares of size 1 meter × 1 meter each. We fix a coordinate system with axes parallel to the sides of the garden. All squares have integer coordinates (x, y) satisfying 1 ≤ x ≤ l, 1 ≤ y ≤ w. Each square may contain any number of roses.
The rectangular areas, which must be selected, should have their sides parallel to the sides of the garden and the squares in their corners should have integer coordinates. For 1 ≤ l1 ≤ l2 ≤ l and 1 ≤ w1 ≤ w2 ≤ w, a rectangular area with corners (l1, w1), (l1, w2), (l2, w1) and (l2, w2):
- contains all the squares with coordinates (x,y) satisfying l1 ≤ x ≤ l2 and w1 ≤ y ≤ w2, and
- has perimeter 2·(l2 − l1 + 1) + 2·(w2 − w1 + 1).
The two rectangular areas must be disjoint, that is they cannot contain a common square. Even if they have a common side, or part of it, they must be surrounded by separate fences.
Write a program, that:
- reads from the standard input the dimensions of the garden, the number of roses in the garden, the number of roses that should be in each of the rectangular areas, and the positions of the roses,
- finds the corners of two such rectangular areas with minimum sum of perimeters that satisfy the given conditions,
- writes to the standard output the minimum sum of perimeters of two
non-overlapping rectangular areas, each containing exactly the given
number of roses (or a single word
NO, if no such pair of areas exists).
Input
The first line of standard input contains two integers: l and w (1 ≤ l,w ≤ 250) separated by a single space - the length and the width of the garden. The second line contains two integers: n and k (2 ≤ n ≤ 5000, 1 ≤ k ≤ n/2) separated by a single space - the number of roses in the garden and the number of roses that should be in each of the rectangular areas. The following n lines contain the coordinates of the roses, one rose per line. The (i+2)nd line contains two integers li, wi (1 ≤ li ≤ l, 1 ≤ wi ≤ w) separated by a single space - the coordinates of the square containing the ith rose. Two or more roses can occur in the same square.In 50% of test cases, the dimensions of the garden will satisfy l,w ≤ 40.
Output
The standard output should contain only one line with exactly one integer
- the minimum sum of perimeters of two non-overlapping rectangular areas,
each containing exactly k roses, or a single word NO, if no such pair of areas
exists.
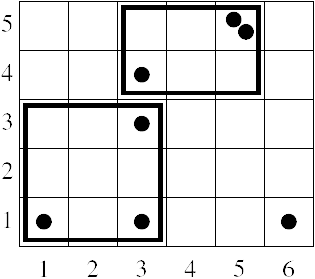
Sample Input6 5 7 3 3 4 3 3 6 1 1 1 5 5 5 5 3 1 Sample Output22 |
|
All Submissions
Best Solutions
Point Value: 30 (partial)
Time Limit: 0.50s
Memory Limit: 32M
Added: Jul 23, 2010
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)