IOI '03 - Kenosha, Wisconsin, USA

Balancing Act

Consider a tree T with N (1 ≤ N ≤ 20,000) nodes numbered 1 … N. Deleting any node from the tree yields a forest: a collection of one or more trees. Define the balance of a node to be the size of the largest tree in the forest T created by deleting that node from T. For example, consider the tree:

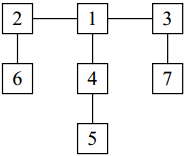
Deleting node 4 yields two trees whose member nodes are {5} and {1, 2, 3, 6, 7}. The larger of these two trees has five nodes, thus the balance of node 4 is five. Deleting node 1 yields a forest of three trees of equal size: {2, 6}, {3, 7}, and {4, 5}. Each of these trees has two nodes, so the balance of node 1 is two.

For an input tree, calculate the node that has the minimum balance. If multiple nodes have equal balance, output the one with the lowest number.

Input Format

The first line of input contains a single integer N. The next N−1 lines contain two space-separated node numbers that are the endpoints of an edge in the tree. No edge will be listed twice, and all edges will be listed.

Output Format

The output should consist of one line with two space-separated integers — the number of the node with minimum balance, and the balance of that node.

Sample Input

7
2 6
1 2
1 4
4 5
3 7
3 1

Sample Output

1 2

All Submissions
Best Solutions

Point Value: 15
Time Limit: 2.00s
Memory Limit: 16M
Added: Apr 13, 2014

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)