King Graff's Trip

King Graff, the ruler of the land of Feerie, is going on a trip through his realm! He would like to give his people a chance to see their great king amongst them, almost as if he too were a petty commoner with no future.

Feerie consists of N (1 ≤ N ≤ 10⁴) towns (numbered 1..N), and M (1 ≤ M ≤ 10⁵) roads. The ith road runs from town A_i to a different town B_i (and can only be travelled in that one direction), and takes T_i (1 ≤ T_i ≤ 10⁹) minutes to traverse. No pair of towns is directly connected by more than one road in the same direction. King Graff will start his trip at town X, and would like to end at a different town Y. Furthermore, since he has better things to do, he would like to complete it in at most L (1 ≤ L ≤ 10¹⁵) minutes.

However, Graff does not like to go long without being worshipped, and the only proper place to do this is in a shrine built to him. S (1 ≤ S ≤ 100) distinct towns contain such shrines - the ith shrine is in town H_i. He would like to minimize the longest continuous stretch of time spent during the trip without passing through any shrines. As the royal computer scientist, your job is to determine the length of this stretch, or break the news to your king that the trip cannot be completed in time. Note that the trip may be impossible to complete in any amount of time, if town Y is not reachable from town X by any path of connected roads.

Input

Line 1: 5 integers, N, M, X, Y, and L
Next M lines: 3 integers, A_i, B_i, and T_i, for i = 1..M
Next line: 1 integer, S
Next S lines: 1 integer, H_i, for i = 1..S

Output

Line 1: 1 integer - the minimum value for the longest continuous stretch of travel time spent away from shrines (in minutes), or -1 if the trip cannot be completed in at most L minutes

Sample Input

5 7 2 3 7
2 3 5
3 2 1
2 1 4
1 3 3
2 4 3
4 5 2
5 3 3
3
1
4
5

Sample Output

4

Explanation of Sample

The map of Feerie is illustrated below:

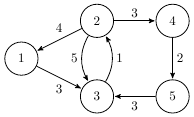
The optimal route goes through towns 2 → 1 → 3, taking 7 minutes with at most 4 minutes spent away from any shrines. The route 2 → 3 is shorter (taking 5 minutes), but has a longer continuous time away from shrines (5). The route 2 → 4 → 5 → 3 has a shorter such value (3), but takes longer than 7 minutes in total (8) and as such is not allowed.

All Submissions
Best Solutions

Point Value: 15 (partial)
Time Limit: 2.00s
Memory Limit: 16M
Added: Sep 12, 2012
Author: SourSpinach

Languages Allowed:
PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, TEXT, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)