COCI 2009/2010, Contest #4

Task PALACINKE

Ana has a couple of classmates coming over for crêpes (known as palačinke in Croatian). They are coming in T minutes, and Ana just found out that she has neither one of the four required ingredients (flour, milk, eggs and jam). She hops into her car and drives around her neighbourhood buying supplies.

Her neighbourhood contains N crossroads numbered 1 to N, and M one way roads connecting them. Ana starts on crossroad 1. On each road there is exactly one shop, selling some, maybe all, ingredients.

Ana needs 1 minute to drive down any given road if she does not stop in the shop, or 2 minutes if she does. She needs to obtain all ingredients and drive back to crossroad one in time. She likes to compare shop prices so she may enter a shop even if she already has all ingredients.

Consider the following example with 5 crossroads and 7 roads.

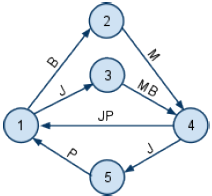
Ana can make the ingredient run in 5 different ways, as shown in the table below.

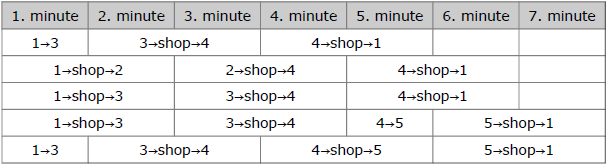
Write a program that will calculate the number of different ways Ana can buy the ingredients and return home in T minutes or less. Since this number can be very large, output it modulo 5557.

Input

The first line contains two integers N and M (1 ≤ N ≤ 25, 1 ≤ M ≤ 500), the number of crossroads and roads.

Each of the next M lines contains two different integers u and v and a string s, separated by exactly one space. They describe a road connecting crossroads u and v, and the shop located on the road selling ingredients s.

The string s will contain between 1 and 4 uppercase characters. Character 'B' for flour, J' for eggs, 'M' for milk and 'P' for jam.

There are at most two direct roads between two crossroads, and only if they are in opposite directions.

The last line contains one integer T (1 ≤ T ≤ 1 000 000 000), the time until Ana's friends arrive, in minutes.

Output

The first and only line of output should contain the number of different ways Ana can buy the ingredients, modulo 5557.

Sample Tests

3 3
1 2 BMJ
2 3 MJP
3 1 JPB
5

3

3 4
1 2 B
2 1 P
1 3 J
3 1 M
8

2

5 7
1 2 B
2 4 M
1 3 J
3 4 MB
4 1 JP
4 5 J
5 1 P
7

5

All Submissions
Best Solutions

Point Value: 25 (partial)
Time Limit: 1.00s
Memory Limit: 32M
Added: Aug 13, 2013

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)