2016 Canadian Computing Olympiad Qualifying Round

Problem Q1: Stupendous Bowties

There are N (1 ≤ N ≤ 100 000) distinct points on a 2D plane, with the i-th one at integral coordinates (x_i, y_i) (−10⁹ ≤ x_i ≤ 10⁹, −10⁹ ≤ y_i ≤ 10⁹).

A Fantastic Right Triangle is one which uses 3 of the given points as its vertices, is non-degenerate (i.e., has positive area), and which has both of its legs axis-aligned (one of its two shortest sides is horizontal and the other shortest side is vertical). The vertex at which the two legs of such a triangle meet (which has an interior right angle) is known as the triangle's Spectacular Vertex.

A Stupendous Bowtie consists of an unordered pair of Fantastic Right Triangles which share the same point as their Spectacular Vertex, and which touch only at that point. Count the number of Stupendous Bowties which exist amongst the given points.

Subtasks

For 2 of the 15 marks available, N ≤ 20.
For another 3 of the 15 marks available, N ≤ 200.
For another 2 of the 15 marks available, N ≤ 2000.
For another 3 of the 15 marks available, N ≤ 100 000, −10⁵ ≤ x_i ≤ 10⁵, and −10⁵ ≤ y_i ≤ 10⁵.

Input Format

The first line of the input contains one integer, N. The remaining N lines each contain two integers, x_i and y_i for i = 1..N.

Output Format

Output a single integer, the number of Stupendous Bowties which exist amongst the given points. Note that this value may not fit in a 32-bit signed integer, and may need to be stored in a long long / long / int64 variable in C++ / Java / Pascal, respectively.

Sample Input

12
-3 6
1 6
-1 4
-3 2
1 2
4 2
-4 -3
-3 -3
1 -3
-1 -4
1 -4
-3 -6

Sample Output

8

Explanation

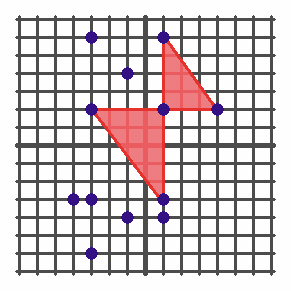
The diagram below illustrates the set of given points (represented by the 12 blue dots), with one of the eight possible Stupendous Bowties shown in red.

All Submissions
Best Solutions

Point Value: 15 (partial)
Time Limit: 2.00s
Memory Limit: 64M
Added: Mar 09, 2016
Author: SourSpinach

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)