2016 Canadian Computing Olympiad

Day 1, Problem 3 - Legends

The country of Canadia consists of a network of cities and roads. Each road can be traversed in both directions. It is possible to get from any city to any other city using the roads.

Suzie studies the creation myths of the Canadiaan people. She is particularly interested in five myths (which correspond to the five subtasks of this problem). The myths are very similar. Each myth has the following form:

In the beginning, Canadia's road network had a particular structure. As time went on, the network was modified to meet the needs of Canadia's growing population. Each modification had one of the following forms:

  • A road was built between two cities that did not yet have a road going directly between them.
  • A new city was built. Cities built in this way were not initially connected to any existing cities.
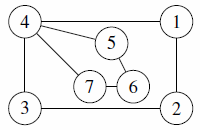
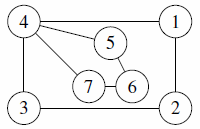
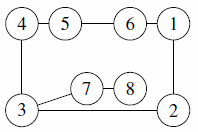
  • A city u grows too large and is split into two cities v and w. The cities originally joined directly to u by a road are partitioned into sets A and B. A road is built from each city in A to v, from each city in B to w and from v to w. For example,

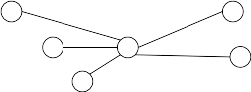 becomes 

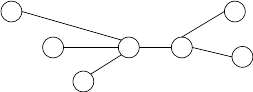
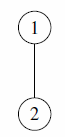
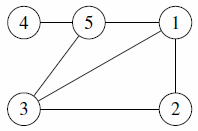
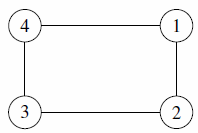
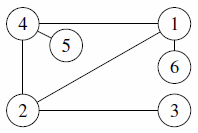
The five myths only differ in the structure that they believe Canadia began with. Here are the original structures, according to each myth:

Subtask 1 [The Myth of the Flask] Subtask 2 [The Myth of the Moon]
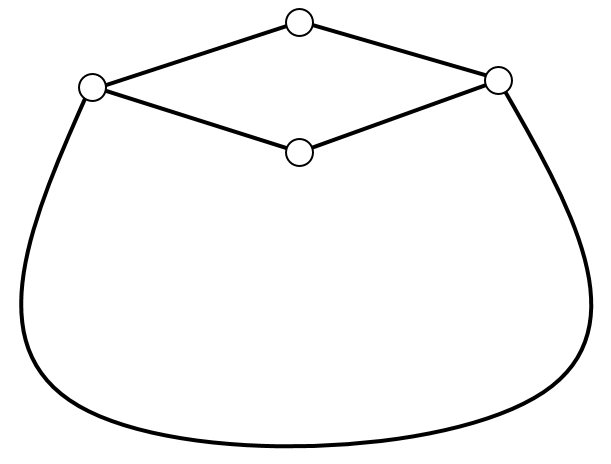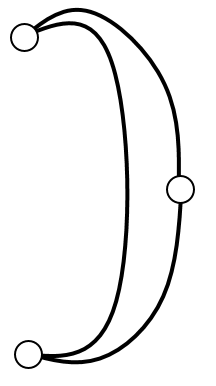Subtask 3 [The Myth of the Sun] Subtask 4 [The Myth of the Eagle's Talon]
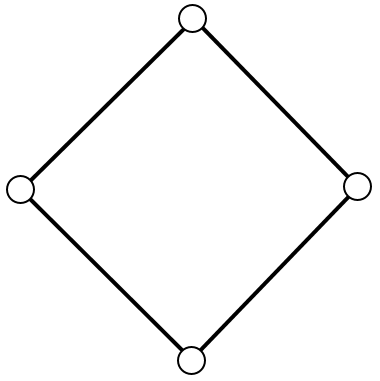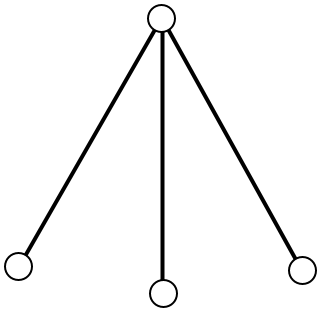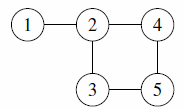
Subtask 5 [The Myth of the Fox]

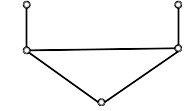For each subtask, you must take the layout of Canadia as input and determine whether the myth might be correct.

Subtasks are worth 5 marks each.

Input Format

The first line contains a single integer S (1 ≤ S ≤ 5) representing the subtask which you must solve.
The second line contains an integer T (1 ≤ T) representing the number of test cases.
Each test case consists of a blank line, followed by two integers N and M (2 ≤ N, 1 ≤ M) representing the number of cities and roads, respectively. The cities are numbered from 1 to N.
Then M lines follow, each containing two integers a and b (1 ≤ a, b ≤ N) representing two cities connected by a road.
No road connects a city to itself. No two roads connect the same pair of cities. It is possible to get from any city to any other city using the roads.

In subtasks 3, you may assume that the sum of N over all test cases is at most 105. In all other subtasks, the sum of N over all test cases is at most 1000.
The same condition holds for M. In particular, in subtask 3, you may assume that the sum of M over all test cases is at most 105. In all other subtasks, the sum of M over all test cases is at most 1000.

Output Format

For each test case, output a single line containing the string YES or the string NO.

Sample Input 1

1
2

4 5
1 2
2 3
3 4
1 3
2 4

7 8
1 2
2 3
3 4
4 1
4 5
5 6
6 7
7 4

Sample Output 1

YES
NO

Explanation 1

Test Case Number Graph Explanation
1 matches The Myth of the Flask
2 cannot match The Myth of the Flask

Sample Input 2

2
2

2 1
1 2

5 6
1 3
5 1
2 3
4 5
1 2
3 5

Sample Output 2

NO
YES

Explanation 2

Test Case Number Graph Explanation
1 cannot match The Myth of the Moon
2 matches The Myth of the Moon, since we can add cities 4 and 5 along with some extra edges to the Moon formed by cities 1, 2 and 3.

Sample Input 3

3
2

7 8
1 2
2 3
3 4
4 1
4 5
5 6
6 7
7 4

8 8
1 2
2 3
3 4
4 5
5 6
6 1
7 3
8 7

Sample Output 3

YES
YES

Explanation 3

Test Case Number Graph Explanation
1 can match The Myth of the Sun, on cities 1, 2, 3 and 4
2 can match The Myth of the Sun, on cities 1, 2, 3 and 4 where some new cities have been inserted between cities 1 and 4

Sample Input 4

4
2

4 4
1 2
2 3
3 4
4 1

6 6
1 2
2 3
1 4
4 5
2 4
1 6

Sample Output 4

NO
YES

Explanation 4

Test Case Number Graph Explanation
1 cannot match The Myth of the Talon
2 can match The Myth of the Talon on cities 1, 2, 4 and 6

Sample Input 5

5
2

5 5
1 2
2 3
2 4
4 5
3 5

6 6
1 2
2 3
1 4
4 5
2 4
1 6

Sample Output 5

NO
YES

Explanation 5

Test Case Number Graph Explanation
1 cannot match The Myth of the Fox
2 can match The Myth of the Fox, on cities 1, 2, 4, 5 and 6

All Submissions
Best Solutions


Point Value: 30 (partial)
Time Limit: 2.00s
Memory Limit: 64M
Added: May 14, 2016
Author: nullptr

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)

It's quiet in here...