2014 Canadian Computing Competition, Stage 1

Problem S4: Tinted Glass Window

You are laying N rectangular pieces of grey-tinted glass to make a stained glass window. Each piece of glass adds an integer value "tint-factor". Where two pieces of glass overlap, the tint-factor is the sum of their tint-factors.

You know the desired position for each piece of glass and these pieces of glass are placed such that the sides of each rectangle are parallel to either the x-axis or the y-axis (that is, there are no "diagonal" pieces of glass).

You would like to know the total area of the finished stained glass window with a tint-factor of at least T.

Input

The first line of input is the integer N (1 ≤ N ≤ 1000), the number of pieces of glass. The second line of input is the integer T (1 ≤ T ≤ 1 000 000 000), the threshold for the tint-factor. Each of the next N lines contain five integers, representing the position of the top-left and bottom-right corners of the i-th piece of tinted glass followed by the tint-factor of that piece of glass. Specifically, the integers are placed in the order x_l y_t x_r y_b t_i, where the top-left corner is at (x_l, y_t) and the bottom-right corner is at (x_r, y_b), and tint-factor is t_i. You can assume that 1 ≤ t_i ≤ 1 000 000. The top-most, left-most co-ordinate where glass can be placed is (0, 0) and you may assume 0 ≤ x_l < x_r ≤ K and 0 < y_t < y_b ≤ K, and

The following additional constraints will apply.

• At least 10% of the marks will be for test cases where N ≤ 100 and K ≤ 100;
• at least 30% of the marks will be for test cases where N ≤ 1000 and K ≤ 1000;
• at least 40% of the marks will be for test cases where N ≤ 100 and K ≤ 1 000 000 000;
• the remaining marks will be for test cases where N ≤ 1000 and K ≤ 1 000 000 000.

Output

Output the total area of the finished stained glass window which has a tint-factor of at least T. All output will be less than 2⁶⁴, and the output for some test cases will be larger than 2³².

Sample Input

4
3
11 11 20 15 1
13 8 14 17 2
17 8 18 17 1
12 12 19 13 1

Sample Output

5

Explanation

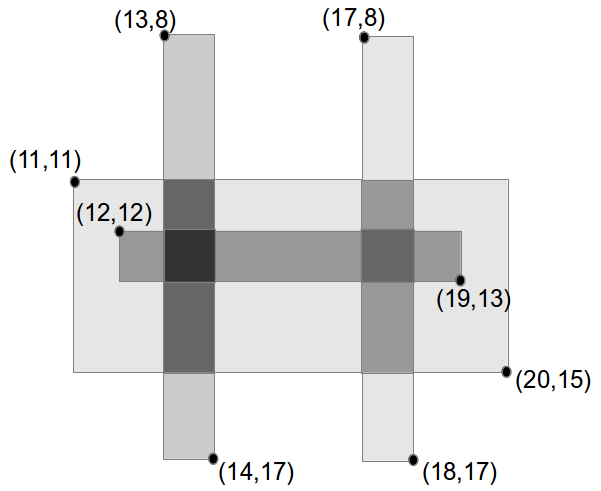
There are 4 pieces of glass used. There are two regions of glass which have a tint-factor greater than or equal to 3: one region between (13, 11) and (14, 15) (which has tint-factor of 3, except for a unit square with tint-factor 4), and another region between (17, 12) and (18, 13) (with tint-factor 3). In total, these two regions have 5 square units of glass with tint-factor greater than or equal to 3, as shown on the diagram below.

All Submissions
Best Solutions

Point Value: 15 (partial)
Time Limit: 2.00s
Memory Limit: 64M
Added: Feb 27, 2014
Author: SourSpinach

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)

I need help with what i might be overlooking, other than the case that its possible to have 1000 by 1000 grid

The coordinates are up to 10^9, so, for starters, they're too large for your array size (to say nothing of the runtime).