2012 Canadian Computing Competition, Stage 2
Day 2, Problem 3: The Winds of War
Colonel Trapp is trapped! For several days he has been fighting General Position on a plateau and his mobile command unit is now stuck at (0, 0), on the edge of a cliff. But the winds are changing! The Colonel has a secret weapon up his sleeve: the "epsilon net." Your job, as the Colonel's chief optimization officer, is to determine the maximum advantage that a net can yield.
The epsilon net is a device that looks like a parachute, which you can launch to cover any convex shape. (A shape is convex when, for every pair p, q of points it contains, it also contains the entire line segment pq.) The net shape must include the launch point (0, 0).
The General has P enemy units stationed at fixed positions and the Colonel has T friendly units. The advantage of a particular net shape equals the number of enemy units it covers, minus the number of friendly units it covers. The General is not a unit.
You can assume that
- no three points (Trapp's position (0, 0), enemy units, and friendly units) lie on a line,
- every two points have distinct x-coordinates and y-coordinates,
- all co-ordinates (x, y) of the units have y > 0,
- all co-ordinates are integers with absolute value at most 1000000000, and
- the total number P + T of units is between 1 and 100
Input Format
The first line contains P and then T, separated by spaces. Subsequently there are P lines of the form x y giving the enemy units' co-ordinates, and then T lines giving the friendly units' coordinates.
Output Format
Output a single line with the maximum possible advantage.
Sample Input
5 3 -8 4 -7 11 4 10 10 5 8 2 -5 7 -4 3 5 6
Sample Output
3
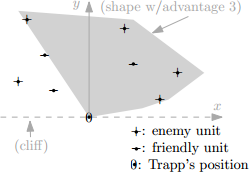
Figure 1: Sample input and an optimal net.
All Submissions
Best Solutions
Point Value: 30 (partial)
Time Limit: 2.00s
Memory Limit: 64M
Added: Jun 20, 2012
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, TEXT, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)