Union Laser
Doctor Y, a leading expert in the field of boxology, is investigating the properties of boxen with his expensive super-precision laser. In particular, he plans to position the laser inside the union of a bunch of axis-aligned boxen, and see where the beam collides with itself.
Since Doctor Y blew all his cash on the laser, he can't actually afford to purchase boxen to conduct his experiment - instead, he will simulate it on his old computer, which uses an integer grid system. He will give his computer an integer N, the number of boxen (1 ≤ N ≤ 10,000), as well as their descriptions. Each box is described by 4 integers - x1, y1, x2 and y2, such that (-3000 ≤ x1, x2 ≤ 3000) and (-3000 ≤ y1, y2 ≤ 3000), where (x1, y1) and (x2, y2) are any two opposite corners of the box. Note that some boxen may have an area of 0 - these do not contribute to the union. He will also input the location of the laser (A, B) such that (-3000 ≤ A, B ≤ 3000) and such that it will be positioned strictly within the box union. The laser points down and right at a 45° angle.
As it turns out, boxen are made of a perfectly reflective material (a fact which Doctor Y will discover upon the completion of his experiment) - as such, whenever the laser beam hits the edge of the box union, it bounces off. For example, if it hits a vertical edge from the left, it bounces to the right, with the up-down direction preserved. If it hits a corner head-on, it will reverse direction, hence colliding with itself right at the corner. Normally, light travels quite fast, but due to the mysterious properties of boxen, the speed of light when inside a box union is only √2 units/second.
Doctor Y plans to use his computer to simulate the paths of the lasers and see when and where they first collide, but there's one problem - the only program on his computer is C++! Offering non-cafeteria food, he lures a desperate Waterloo student into his lab, where he forces him (or her?) to write the laser simulation program. That's you!
Input
| Line 1: | A single integer - N |
| Line 2: | Two integers - A and B |
| The next N lines: | Four integers - x1, y1, x2 and y2 |
Output
If the laser beam never collides with itself of the laser, simply output "Time limit exceeded".
If the laser beam collides with the actual laser before it collides with itself, the first line of output should consist of a single number - the amount of time that passes before the laser beam collides with the laser, in seconds. The second line should read "Broken equipment".
Otherwise, the first line of output should consist of a single number - the amount of time that passes before laser beam first collides with itself, in seconds. The second line should contain a pair of numbers - the X and Y coordinates of where this takes place, respectively.
Each number should be rounded off to 1 decimal place.
Sample Input
7 0 4 -1 -1 1 5 0 -2 4 2 0 2 1 -4 5 -4 2 -1 5 2 7 4 3 -5 4 -4 0 -6 3 -4
Sample Output
12.0 0.0 0.0
Explanation
The grid looks like this:
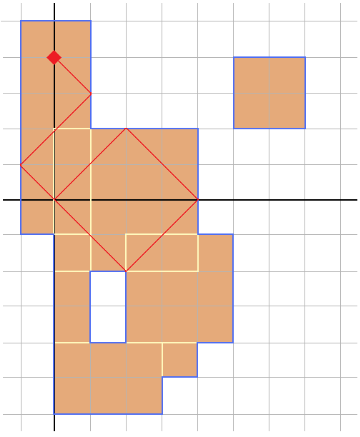
The filled-in squares represent squares that are part of at least one box - together, they make up the box union. Note that the union can have holes in it, and that it can be disjoint.
The blue lines denote the boundaries of the union - these are the lines that the laser can bounce off of.
The yellow lines are edges of boxen that do not contribute to the union - the laser can go through these freely.
The red diamond is the position of the laser, and the red line is the path that the laser beam follows.
Note that when it bounces off the corner at (2, -2), since it didn't hit it head-on, it is the same as bouncing off of a horizontal edge.
Following the path of the laser beam, it can be seen that it collides with itself at (0, 0). Before this, it has travelled 12√2 units, which takes exactly 12 seconds.
More Examples
If the laser were positioned at (0, 3), the output should be:
12.0 0.0 -1.0
If the laser were positioned at (0, 1), the output should be:
5.0 5.0 -4.0
If the laser were positioned at (0, 0), the output should be:
8.0 Broken equipment
All Submissions
Best Solutions
Point Value: 25 (partial)
Time Limit: 2.00s
Memory Limit: 256M
Added: May 17, 2009
Author: SourSpinach
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)
Firstly, now boxen of area 0 are allowed - but they do not contribute to the box union, and as such can be ignored.
Secondly, (x1,y1) and (x2,y2) now represent any two opposite corners of a box - this means that x1 can be larger than x2, and y1 can be larger than y2.
These are 4 out of the 5 cases where boxes have 0 area( x1==x2 or y1==y2)
I don't see why there should be boxes with no area to begin with, but these boxes don't change the box union in my program, so it might be a problem with the judge, or the problem statement.
... or something I missed despite debugging
Can the laser travel inside of empty boxes or something which wasn't clear?
Only the author has a correct solution, so I can't be sure.
As for the data itself, I don't know what I was smoking when I wrote the test case generator, but it does indeed allow for boxen of area 0. I'll fix the cases in which this occurs - since you've figured it out already, would you mind telling me which 5 they are?
Sorry about these errors - how very embarrassing.
cases 8-11 are the 4 I get wrong..
there aren't many special cases, so I can't figure out what they are.
All test data laser starts completely surrounded by boxen, so that isn't it... 3 samples seem to be correct for me... I can't figure it out.
cases like
XL
.X don't even seem to occur in test data, so that doesn't seem to be it(down,left between two gaps to a box)
y1<=y2 is not true (5 > -1), though it should be.
Could cause bugs in programs if it is assumed but not true
I don't believe this happens in any of the actual data.