Boxdropper
The University of Waterloo is famous for its booming population of geese, and many researchers go there to study them. One day, Doctor Y (known for his work in the field of boxology) decided to go there and investigate how good geese are at optimization problems.
At UW there is a large lake (so large, in fact, that the boundaries are never an issue). Doctor Y decides to drop a number of 2D boxen onto this lake and command the geese to travel from one to another, recording how much time they spend flying as opposed to walking (naturally, the geese won't swim, considering the not-so-appealing brown colour of the lake). He has a Boxdropper machine at his disposal to do the work for him - he can give it the following commands:
| B x1 y1 x2 y2 | Drop a box onto the lake such that its lower-left coordinate is at (x1, y1) and its upper-right coordinate is at (x2, y2). Doctor Y defines to the origin to be somewhere in the middle of the lake. Note that boxen can overlap one another. |
| G a b | Command the geese to travel from the ath box dropped to the bth one, and record the total distance that they fly. |
Since the scientific community has not yet realized the benefits of studying boxen, Doctor Y isn't receiving much funding - as such, he only has 500 boxen at his disposal, and his machine can only handle 1,000,000 commands before it overheats. In cases worth 50% of the total points, he doesn't even have enough funding to purchase a fully functional Boxdropper - in these cases, all of the B commands will come first, followed by all of the G commands.
The geese can walk across boxen freely, but sometimes they may have to fly over water to reach other boxen. The geese, secretly participating in the second stage of the Canadian Computing Competition every year, are well versed in optimization problems such as these, and so will always choose a path that will minimize the total distance that they spend flying. Given the commands that Doctor Y inputs into the Boxdropper, determine the distances recorded by it (one for every G command).
Input
On each line, one of 3 commands will be given:
If the line starts with the character B, it will be followed by 4 integers (x1, y1, x2, and y2), with (-1,000,000 ≤ x1, x2 ≤ 1,000,000) and (-1,000,000 ≤ y1, y2 ≤ 1,000,000).
If the line starts with the character G, it will be followed by 2 integers a and b, (a ≠ b and 1 ≤ a, b ≤ n), where n is the number of B commands so far.
Output
For every G command, output the distance that the geese spend flying. The numbers should be printed one per line, and rounded off to 3 decimal places.
Sample Input
B -1 2 1 5 B 3 -4 4 1 G 2 1 B 4 -3 6 -2 B 6 -6 8 -4 G 2 3 G 1 4
Sample Output
2.236 0.000 3.236
Explanation
The lake looks like this:
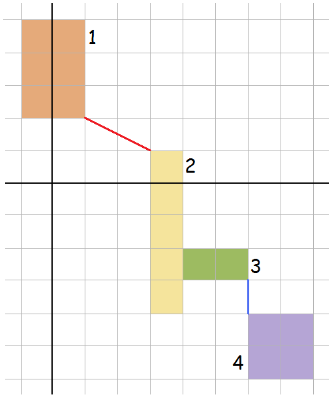
For the first G command, the geese must fly along the red line, which has a length of √5.
For the second, the two boxen are touching, so no flight is necessary.
For the third, the geese must first fly along the red line, then walk across boxen 2 and 3, and finally fly along the blue line, which has a length of 1.
All Submissions
Best Solutions
Point Value: 20 (partial)
Time Limit: 5.00s
Memory Limit: 64M
Added: May 15, 2009
Author: SourSpinach
Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3










Comments (Search)