Asia-Pacific Informatics Olympiad 2008

Problem 2: Roads

The Kingdom of New Asia contains N villages connected by M roads. Some roads are made of cobblestones, and others are made of concrete. Keeping roads free-of-charge needs a lot of money, and it seems impossible for the Kingdom to maintain every road. A new road maintaining plan is needed.

The King has decided that the Kingdom will keep as few free roads as possible, but every two distinct villages must be connected by one and only one path of free roads. Also, although concrete roads are more suitable for modern traffic, the King thinks walking on cobblestones is interesting. As a result, he decides that exactly K cobblestone roads will be kept free.

For example, suppose the villages and the roads in New Asia are as in Figure 1a. If the King wants to keep two cobblestone roads free, then the Kingdom can keep roads (1,2), (2,3), (3,4), and (3,5) free as in Figure 1b. This plan satisfies the King's criteria because (1) every two villages are connected via one and only one path of free roads, (2) there are as few free roads as possible, and (3) there are exactly two cobblestone roads: (2,3) and (3,4).

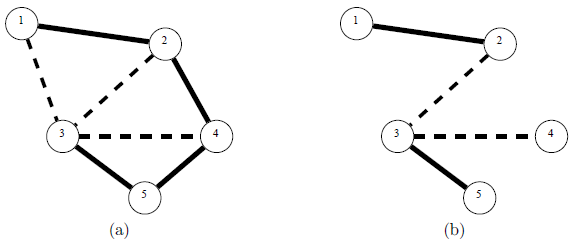
Figure 1: (a) An example configuration of villages and roads in the Kingdom of New Asia. Solid lines denote concrete roads, and dashed lines denote cobblestone roads. (b) A road maintaining plan that keeps two cobblestone roads free. Only free roads are shown.

Task

Given a description of roads in New Asia and the number of cobblestone roads that the King wants to keep free, write a program to determine if there is a road maintaining plan that satisfies the King's criteria, and output a valid plan if there is one.

Input

The first line contains three integers separated by one space:

• N, the number of villages (1 ≤ N ≤ 20,000)
• M, the number of roads (1 ≤ M ≤ 100,000)
• K, the number of cobblestone roads the King wants to keep free (0 ≤ K ≤ N - 1)

The following M lines describes the roads in New Asia, which are numbered 1 to M. The (i + 1)st line describes Road i. It contains three intergers separated by one space:

• u_i and v_i, the two villages connected by road i. Villages are numbered 1 to N
• c_i, the type of road i; c_i = 0 if road i is made of cobblestone, and c_i = 1 if it is made of concrete.

There will be no more than one road connecting a pair of villages.

Output

If there is no road maintaining plan that satisfies the King's criteria, your program should print no solution on the first line of the output.

Otherwise, your program should output a valid road maintaining plan by listing roads that will be kept free, one road per line. To list a road, print the line in the input that describes it. The roads can be listed in any order. If there are more than one valid plan, you can output any such plan.

Sample Input

5 7 2
1 3 0
4 5 1
3 2 0
5 3 1
4 3 0
1 2 1
4 2 1

(This input agrees with Figure 1a.)

Sample Output

3 2 0
4 3 0
1 2 1
5 3 1

(This output agrees with Figure 1b.)

Scoring

The score for each input scenario will be 100% if the correct answer is outputed and 0% otherwise. In test scenarios worthing 20 points, K will be at most 10.

All Submissions
Best Solutions

Point Value: 20
Time Limit: 1.00s
Memory Limit: 128M
Added: May 05, 2009

Languages Allowed:
C++03, PAS, C, HASK, ASM, RUBY, PYTH2, JAVA, PHP, SCM, CAML, PERL, C#, C++11, PYTH3

Comments (Search)