Difference between revisions of "Range minimum query"

Revision as of 05:35, 21 November 2011

The term range minimum query (RMQ) comprises all variations of the problem of finding the smallest element in a contiguous subsequence of a list of items taken from a totally ordered set (usually numbers). This is one of the most extensively-studied problems in computer science, and many algorithms are known, each of which is appropriate for a specific variation.

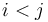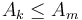A single range minimum query is a set of indices $i < j$ into an array $A$ ; the answer to this query is some $k \in [i,j]$ such that $A_k \leq A_m$ for all $m \in [i,j]$ . In isolation, this query is answered simply by scanning through the range given and selecting the minimum element, which can take up to linear time. The problem is interesting because we often desire to answer a large number of queries, so that if, for example, 500000 queries are to be performed on a single array of 10000000 elements, then using this naive approach on each query individually is probably too slow.

Static

In the static range minimum query, the input is an array and a set of intervals (contiguous subsequences) of the array, identified by their endpoints, and for each interval we must find the smallest element contained therein. Modifications to the array are not allowed, but we must be prepared to handle queries "on the fly"; that is, we might not know all of them at once.

Sliding

This problem can be solved in linear time in the special case in which the intervals are guaranteed to be given in such an order that they are successive elements of a sliding window; that is, each interval given in input neither starts earlier nor ends later than the previous one. This is the sliding range minimum query problem; an algorithm is given in that article.

Division into blocks

In all other cases, we must consider other solutions. A simple solution for this and other related problems involves splitting the array into equally sized blocks (say, 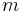$m$ elements each) and precomputing the minimum in each block. This precomputation will take 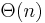$\Theta(n)$ time, since it takes 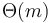$\Theta(m)$ time to find the minimum in each block, and there are 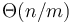$\Theta(n/m)$ blocks.

After this, when we are given some query $[a,b]$ , we note that this can be written as the union of the intervals $[a,c_0), [c_0, c_1), [c_1, c_2), ..., [c_{k-1}, c_k), [c_k, b]$ , where all the intervals except for the first and last are individual blocks. If we can find the minimum in each of these subintervals, the smallest of those values will be the minimum in $[a,b]$ . But because all the intervals in the middle (note that there may be zero of these if $a$ and $b$ are in the same block) are blocks, their minima can simply be looked up in constant time.

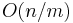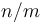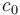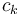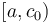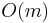Observe that the intermediate intervals are $O(n/m)$ in number (because there are only about $n/m$ blocks in total). Furthermore, if we pick $c_0$ at the nearest available block boundary, and likewise with $c_k$ , then the intervals $[a,c_0)$ and $[c_k,b]$ have size $O(m)$ (since they do not cross block boundaries). 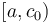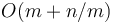By taking the minimum of all the precomputed block minima, and the elements in $[a,c_0)$ and $[c_k,b]$ , the answer is obtained in $O(m + n/m)$ time. If we choose a block size of 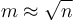$m \approx \sqrt{n}$ , we obtain 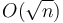$O(\sqrt{n})$ overall.

Segment tree

While 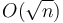$O(\sqrt{n})$ is not optimal, it is certainly better than linear time, and suggests that we might be able to do better using precomputation. Instead of dividing the array into 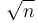$\sqrt{n}$ pieces, we might consider dividing it in half, and then dividing each half in half, and dividing each quarter in half, and so on. The resulting structure of intervals and subintervals is a segment tree. It uses linear space and requires linear time to construct; and once it has been built, any query can be answered in 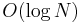$O(\log N)$ time.

Sparse table

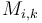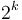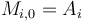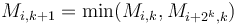(Name due to ^[1].) At the expense of space and preprocessing time, we can even answer queries in $O(1)$ using dynamic programming. Define $M_{i,k}$ to be the minimum of the elements $A_i, A_{i+1}, ..., A_{i+2^k-1}$ (or as many of those elements as actually exist); that is, the elements in an interval of size $2^k$ starting from $i$ . Then, we see that $M_{i,0} = A_i$ for each $i$ , and $M_{i,k+1} = \min(M_{i,k}, M_{i+2^k,k})$ ; that is, the minimum in an interval of size 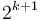$2^{k+1}$ is the smaller of the minima of the two halves of which it is composed, of size 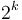$2^k$ . 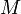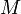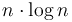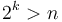Thus, each entry of $M$ can be computed in constant time, and in total $M$ has about $n\cdot \log n$ entries (since values of $k$ for which $2^k > n$ are not useful). Then, given the query $[a,b]$ , simply find $k$ such that 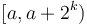$[a,a+2^k)$ and $(b-2^k,b]$ overlap but are contained within $[a,b]$ ; then we already know the minima in each of these two sub-intervals, and since they cover the query interval, the smaller of the two is the overall minimum. 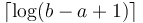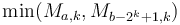It's not too hard to see that the desired $k$ is $\lceil\log(b-a+1)\rceil$ ; and then the answer is $\min(M_{a,k}, M_{b-2^k+1,k})$ .