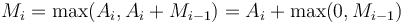Difference between revisions of "Maximum subvector sum"
| Line 12: | Line 12: | ||
===Implementation (C++)=== | ===Implementation (C++)=== | ||
<syntaxhighlight lang="cpp"> | <syntaxhighlight lang="cpp"> | ||
| − | int max_subvector_sum( | + | template<class Vector> |
| + | int max_subvector_sum(Vector V) | ||
{ | { | ||
int res = 0, cur = 0; | int res = 0, cur = 0; | ||
| Line 22: | Line 23: | ||
==Higher dimensions== | ==Higher dimensions== | ||
| − | The obvious generalization of the problem is as follows: given a <math>d</math>-dimensional array of dimensions <math>n_1 \ | + | The obvious generalization of the problem is as follows: given a <math>d</math>-dimensional array (or ''tensor'') of dimensions <math>n_1 \leq n_2 \leq \ldots \leq n_d</math>, find indices <math>1 \leq a_1 \leq b_1 \leq n_1, 1 \leq a_2 \leq b_2 \leq n_2, \ldots, 1 \leq a_d \leq b_d \leq n_d</math> such that the sum <math>\sum_{i_1=a_1}^{b_1} \sum_{i_2=a_2}^{b_2} \ldots \sum_{i_d=a_d}^{b_d} A_{i_1, i_2, \ldots, i_d}</math> is maximized (or return 0 if all entries are negative). If we imagine a two-dimensional array as a matrix, then the problem is to pick some axis-aligned rectangle within the matrix with maximum sum. |
| − | + | We describe a simple algorithm for this problem. It works by recursively reducing a <math>d</math>-dimensional problem to <math>O(n_1^2)</math> simpler, <math>(d-1)</math>-dimensional problems, terminating at <math>d=1</math> which can be solved in <math>O(n_d)</math> time using the one-dimensional algorithm. Evidently, this algorithm takes time <math>O(n_1^2 n_2^2 \ldots n_{d-1}^2 n_d)</math>. In the case with all dimensions equal, this reduces to <math>O(n^{2d-1})</math>, or <math>O(n^3)</math> in the two-dimensional case. | |
| − | + | The details are as follows. We try all possible sets of bounds <math>[a_1, b_1] \in [1, n_1]</math> for the last index. For each such interval, we create a <math>(d-1)</math>-dimensional tensor <math>B</math> where <math>B_{i_2, i_3, \ldots, i_d} = \sum_{i_1=a_1}^{b_1} A_{i_1, i_2, \ldots, i_d}</math> and compute the maximum subtensor sum in <math>B</math>. The range of indices that this represents in the original array will be the Cartesian product of the indices in the maximum-sum subtensor of <math>B</math> and the original range <math>[a_1, b_1]</math>, so that by trying all possibilities for the latter, we will account for all possible subtensors of the original array <math>A</math>. | |
| + | |||
| + | This algorithm is not [[asymptotically optimal]]; for example, the <math>d=2</math> case can be solved in <math>O(n^3 (\log n)/(\log \log n))</math> time by a result due to Takaoka.<ref name="takaoka"/> This implies that for <math>d > 1</math>, we can always achieve <math>O(n^{2d-1} (\log n)/(\log \log n))</math>, which is slightly better than the algorithm given above. In practice, however, the gains are not large. | ||
==Problems== | ==Problems== | ||
Revision as of 23:02, 19 April 2012
The maximum subvector sum problem is that of finding a segment of a vector (array of numbers)[1], possibly empty, with maximum sum. If all elements of the array are nonnegative, then the problem may be trivially solved by taking the entire vector; if all elements are negative, then the problem is again trivially solved by taking the empty segment (whose sum is conventionally defined to be zero). The problem requires more thought, however, when the vector contains a mixture of positive and negative numbers.
This problem originated in the domain of image processing;[2] applications have also been found in data mining.[3] In algorithmic programming competitions, Kadane's linear time algorithm for this problem is often useful as a building block within a more complex algorithm for processing a multidimensional array.
Contents
One-dimensional problem
Bentley[2] describes four algorithms for this problem, of running time 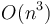 ,
, 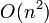 ,
, 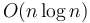 , and
, and 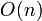 . We discuss only the latter in this article, which is known as Kadane's algorithm after its discoverer.
. We discuss only the latter in this article, which is known as Kadane's algorithm after its discoverer.
Kadane's algorithm is a classic example of dynamic programming. It works by scanning the vector from left to right and computing the maximum-sum subvector ending at each of the vector's entries; denote the best sum ending at entry  by
by 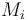 . Also, for convenience, set
. Also, for convenience, set 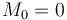 for the empty subvector. The maximum subvector sum for the entire array
for the empty subvector. The maximum subvector sum for the entire array  is then, of course,
is then, of course, 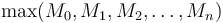 .
. 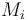 for
for 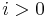 may then be computed as follows:
may then be computed as follows:
This formula is based on the following optimal substructure: The maximum-sum subvector ending at position  consists of either only the element
consists of either only the element 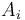 itself, or that element plus one or more elements
itself, or that element plus one or more elements 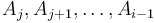 (that is, ending at the previous position
(that is, ending at the previous position 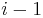 ). But the sum obtained in the latter case is simply
). But the sum obtained in the latter case is simply 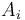 plus the sum of the subvector ending at
plus the sum of the subvector ending at 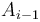 , so we want to make the latter as great as possible, requiring us to choose the maximum-sum subvector ending at
, so we want to make the latter as great as possible, requiring us to choose the maximum-sum subvector ending at 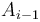 . This accounts for the
. This accounts for the 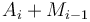 term. Of course, if
term. Of course, if 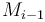 turned out to be negative, then there is no point in including any terms before
turned out to be negative, then there is no point in including any terms before 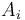 at all. This is why we must take the greater of
at all. This is why we must take the greater of 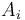 and
and 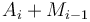 .
.
Implementation (C++)
template<class Vector> int max_subvector_sum(Vector V) { int res = 0, cur = 0; for (int i = 0; i < V.size(); i++) res = max(res, cur = V[i] + max(0, cur)); return res; }
Higher dimensions
The obvious generalization of the problem is as follows: given a 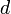 -dimensional array (or tensor) of dimensions
-dimensional array (or tensor) of dimensions 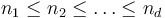 , find indices
, find indices 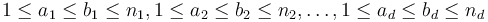 such that the sum
such that the sum 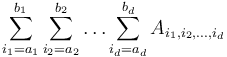 is maximized (or return 0 if all entries are negative). If we imagine a two-dimensional array as a matrix, then the problem is to pick some axis-aligned rectangle within the matrix with maximum sum.
is maximized (or return 0 if all entries are negative). If we imagine a two-dimensional array as a matrix, then the problem is to pick some axis-aligned rectangle within the matrix with maximum sum.
We describe a simple algorithm for this problem. It works by recursively reducing a 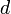 -dimensional problem to
-dimensional problem to 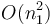 simpler,
simpler,  -dimensional problems, terminating at
-dimensional problems, terminating at 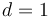 which can be solved in
which can be solved in 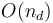 time using the one-dimensional algorithm. Evidently, this algorithm takes time
time using the one-dimensional algorithm. Evidently, this algorithm takes time  . In the case with all dimensions equal, this reduces to
. In the case with all dimensions equal, this reduces to 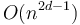 , or
, or 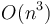 in the two-dimensional case.
in the two-dimensional case.
The details are as follows. We try all possible sets of bounds ![[a_1, b_1] \in [1, n_1]](/wiki/images/math/9/d/8/9d8521863967c62da8b3c41d5e7468f6.png) for the last index. For each such interval, we create a
for the last index. For each such interval, we create a  -dimensional tensor
-dimensional tensor  where
where 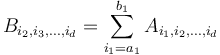 and compute the maximum subtensor sum in
and compute the maximum subtensor sum in  . The range of indices that this represents in the original array will be the Cartesian product of the indices in the maximum-sum subtensor of
. The range of indices that this represents in the original array will be the Cartesian product of the indices in the maximum-sum subtensor of  and the original range
and the original range ![[a_1, b_1]](/wiki/images/math/1/f/2/1f2bdcb8e76f233ce0b0677c8a8fc80e.png) , so that by trying all possibilities for the latter, we will account for all possible subtensors of the original array
, so that by trying all possibilities for the latter, we will account for all possible subtensors of the original array  .
.
This algorithm is not asymptotically optimal; for example, the 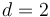 case can be solved in
case can be solved in 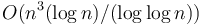 time by a result due to Takaoka.[3] This implies that for
time by a result due to Takaoka.[3] This implies that for 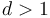 , we can always achieve
, we can always achieve 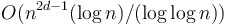 , which is slightly better than the algorithm given above. In practice, however, the gains are not large.
, which is slightly better than the algorithm given above. In practice, however, the gains are not large.
Problems
Notes and references
- ↑ In computer science, vector is often used to mean array of real numbers; sometimes it is simply synonymous with array. Here, array is used in contradistinction with linked list, which does not support efficient random access. This meaning is related to but different from the meaning of the word in mathematics and physics.
- ↑ 2.0 2.1 Bentley, Jon (1984), "Programming pearls: algorithm design techniques", Communications of the ACM 27 (9): 865–873, doi:10.1145/358234.381162.
- ↑ 3.0 3.1 Takaoka, T. (2002), "Efficient algorithms for the maximum subarray problem by distance matrix multiplication", Electronic Notes in Theoretical Computer Science 61.