Array
The array is a data structure considered fundamental in imperative programming languages. We shall take the definition of the term to be a collection of objects, all of the same size and type, regularly spaced in random-access memory (RAM). Because the objects are regularly spaced in memory, their addresses occur in arithmetic progression. Therefore, when we assign the object at the lowest memory address an index of, for example, zero, the next object after that an index of one, and so on up to the  th object, which receives an index of
th object, which receives an index of 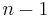 , we can access any object in the array in constant time just by knowing the index (using the formula for the
, we can access any object in the array in constant time just by knowing the index (using the formula for the  th term of an arithmetic progression). This property makes the array data structure useful and applicable to a wide variety of different algorithms, and many other data structures contain arrays, using them to organize information internally. In particular, an array is often the ideal data structure for a finite sequence.
th term of an arithmetic progression). This property makes the array data structure useful and applicable to a wide variety of different algorithms, and many other data structures contain arrays, using them to organize information internally. In particular, an array is often the ideal data structure for a finite sequence.
In functional programming languages based upon the lambda calculus, arrays are not fundamental ingredients, as the lambda calculus is not aware of the organization of computer memory. Nevertheless, they may have language support for the sake of efficiency.
In some programming languages (notably PHP), all arrays are associative by default. An associative array is not a type of array, but a more complex data structure named in analogy to the array.
Contents
Terminology
The size of an array is the number of objects it contains. The stored objects themselves are known as elements, entries, or values of the array. An element of an array is uniquely identified in that array by an index, which is usually a natural number (as in the preceding paragraph), but may be any kind of object taken from a finite well-ordered set. (For example, the Pascal programming language allows the use of characters as array indices, as characters may be well-ordered according to their ASCII values; it allows boolean indices, with false = 0 and true = 1; but it does not allow reals. All programming languages that support arrays support natural numbers as indices, and some do not support any other type of index.) Indices do not appear in the array itself; the choice of index is an arbitrary convention we use to abstract the locations of elements in arrays, without using the addresses themselves, which can be cumbersome to work with and may change every time a program is run and memory for the array allocated. If an element of an array is located at index  , the element immediately following it in the array, if there is one, occurs at an index equal to the successor of
, the element immediately following it in the array, if there is one, occurs at an index equal to the successor of  ; if
; if  is an integer then this is
is an integer then this is 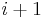 .
.
A segment or slice of an array consists of exactly those values of the array occurring at indices taken from a contiguous range. For example, we may choose the entire array, or we may choose no elements at all, or we may choose the fifth element, or we may choose the ninth, tenth, eleventh, and twelfth elements; all these are considered segments or slices.
Indexing convention
The vast majority of arrays encountered in practice are zero-indexed or zero-based; that is, they are indexed with consecutive natural numbers starting from zero. This is probably due to the influence of C, in which arrays are formalisms constructed over pointers to their initial elements and indices are merely offsets, so that index 0 represents the initial element itself.
In theoretical contexts, arrays are again often zero-indexed, but are also often one-based or one-indexed, that is, indexed with consecutive natural numbers starting from one. The author usually chooses whichever is more convenient.
Also, note that sometimes a zero-indexed array used in practice is treated as a one-indexed array, and the element at index zero is not used, or it is allowed to exist only for the sake of convenience, i.e., as a sentinel value, or a buffer against out-of-bounds accesses.
Address computation
If each element in an array occupies  bytes of memory, then the difference in addresses of consecutive elements in the array is some value
bytes of memory, then the difference in addresses of consecutive elements in the array is some value 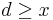 . It may be exactly
. It may be exactly  , in which case the array takes up exactly the same amount of space as its individual elements combined, but, depending on the programming language,
, in which case the array takes up exactly the same amount of space as its individual elements combined, but, depending on the programming language, 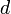 may also be somewhat greater than
may also be somewhat greater than  in order to keep the elements word-aligned. (In practice, most compilers will not choose
in order to keep the elements word-aligned. (In practice, most compilers will not choose 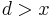 , simply because it wastes space.)
, simply because it wastes space.)
Now, suppose this array is indexed by members of some finite well-ordered set 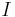 . Define a bijection
. Define a bijection  between
between 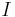 and
and 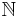 (starting from zero) as follows: since
(starting from zero) as follows: since 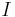 is well-ordered, it has a least element
is well-ordered, it has a least element  ; we shall write
; we shall write 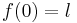 . Then, either
. Then, either 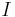 is exhausted, or it contains a next smaller element,
is exhausted, or it contains a next smaller element, 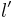 ; then we shall write
; then we shall write 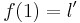 , and so on until the elements of
, and so on until the elements of 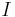 have been put into order in one-to-one correspondence with
have been put into order in one-to-one correspondence with 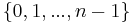 (where
(where 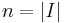 ).
).
Furthermore, suppose that the first element in the array, the element located at the lowest memory address, in fact has address  . Then the element located at index
. Then the element located at index  will have address
will have address 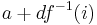 . Likewise, if we know the address
. Likewise, if we know the address 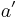 of an element, then its index is given by
of an element, then its index is given by 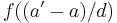 .
.
For example, suppose that a program is counting the number of words that start with each letter of the Latin alphabet. Then it will probably have an array indexed by the alphabet in which the values are, say, integers 4 bytes long. So the element at index a holds the number of words that start with a, the element at index b holds the number of words that start with b, and so on up to z. Then, we will have 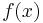 defined to be the
defined to be the 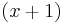 th letter of the alphabet, hence
th letter of the alphabet, hence 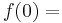 a, ...,
a, ..., 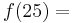 z.
So suppose that the first element of the array (the count of words starting with a) has address 92631507. Then, suppose we wish to look up the number of words starting with the letter s. s is the 19th letter of the alphabet, so we will find this entry at address 92631507+4×18 = 92631579. Likewise, suppose we wish to know which element is located at address 92631555. To do this, we let
z.
So suppose that the first element of the array (the count of words starting with a) has address 92631507. Then, suppose we wish to look up the number of words starting with the letter s. s is the 19th letter of the alphabet, so we will find this entry at address 92631507+4×18 = 92631579. Likewise, suppose we wish to know which element is located at address 92631555. To do this, we let 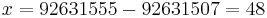 , whence
, whence 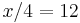 and the index we seek is
and the index we seek is 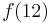 , the thirteenth letter of the alphabet, which is m. (This example illustrates that it's really not as complicated as it sounds; the mapping of indices to addresses is very intuitive.)
, the thirteenth letter of the alphabet, which is m. (This example illustrates that it's really not as complicated as it sounds; the mapping of indices to addresses is very intuitive.)
Multidimensional arrays
The visual interpretation of the array is, perhaps, a line of boxes, each of which is a variable (a space in memory that holds one of the array's elements). So, for example, suppose there were fifty people in a line and we wanted to store their names. Then we could assign each person a number according to his or her position in the line, and use these as indices to an array with 50 elements, each of which holds the name of one person (presumably as a fixed-length string or a pointer to a variable-length string)?
It becomes clear fairly quickly, however, that this mode of thinking is severely limiting. For example, suppose that there are 50 rows of 50 occupied chairs each, and we want to store the names of all 2500 people listening to a speech. What do we do now? One method is to imagine that we asked the first row to stand up and form a line off to the left side, then we asked the second row to stand up and line up behind the people who used to be in the first row, in such a way that if Alice is originally seated to the left of Bob, she will end up in front of Bob in the line; and so on down until all 2500 people have lined up, and we assign the number 0 to the first person in the line, 1 to the second person, and eventually 2499 to the last person. (In a bird's eye view facing the podium, we are assigning IDs in English reading order: left to right then top to bottom.) Then we could use an array indexed by the integers from 0 to 2499 to hold information about the names of all the people attending.
But this is cumbersome. Suppose that the guest sitting in the 12th row and the 34th column is randomly selected to win a prize, and we wish to call him out by name. Then we have to compute that his ID is 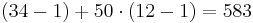 , and look up the array element at index 583. It would be much more convenient if we could simply use the ordered pair
, and look up the array element at index 583. It would be much more convenient if we could simply use the ordered pair 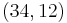 as an index --- not a location along a line, but the coordinates of a point in a plane. The array is being used, after all, to represent a table or matrix or grid of things, not a line.
as an index --- not a location along a line, but the coordinates of a point in a plane. The array is being used, after all, to represent a table or matrix or grid of things, not a line.
First solution
This, in fact, is the principle behind a multidimensional array, an array indexed by  -tuples, where
-tuples, where 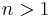 . (Such an array is said to be
. (Such an array is said to be  -dimensional.) It is not hard to form a bijection between tuples and
-dimensional.) It is not hard to form a bijection between tuples and 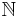 ; in this example, we have a two-dimensional array with
; in this example, we have a two-dimensional array with  ,
,  , ...,
, ...,  ,
,  , ...,
, ...,  , ...,
, ..., 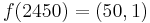 , ...,
, ...,  . The point is that, in order to ease the cognitive burden on the programmer and aid visualization, the details of the address translation should be taken care of by the compiler and hidden from the programmer. Many programming languages support arrays with several dimensions; these are particularly important in dynamic programming. The size of a multidimensional array is the product of the sizes of the individual sets whose Cartesian product was taken to form the set of tuples as indices for the array. The elements of the tuple need not be all of the same type.
. The point is that, in order to ease the cognitive burden on the programmer and aid visualization, the details of the address translation should be taken care of by the compiler and hidden from the programmer. Many programming languages support arrays with several dimensions; these are particularly important in dynamic programming. The size of a multidimensional array is the product of the sizes of the individual sets whose Cartesian product was taken to form the set of tuples as indices for the array. The elements of the tuple need not be all of the same type.
Second solution
Instead of allowing tuples as indices, we could, in fact, simply allow the use of more than one index to an array. A two-dimensional array will be considered as a one-dimensional array of one-dimensional arrays. A three-dimensional array will be considered a one-dimensional array of one-dimensional arrays of one-dimensional arrays. And so on. After all, we did not place any restrictions on the value types of arrays! In the example above, then, each row is viewed as an array of 50 strings, and the whole arrangement is viewed as an array of 50 rows. To access the person in row 12 and column 34, we take the 34th element of the 12th element of the array.
Programming languages that take this approach to multidimensional arrays generally allow extraction of the lower-dimensional components, thus, the entire first row could be extracted and passed as an argument to a function, for example. In the first solution (tuple indices), these are slices.
Note on interpretation
(It is important to remember that a multidimensional array is still, in a sense, a line of values sitting in memory, and that the convention of indexing them by tuples is only for convenience and has no real existence within the machine. Accordingly, the interpretation of the array determines its abstract nature, and not vice versa; whether the first element of an ordered pair as the index represents the row or the column is irrelevant as long as one is consistent, and they may represent, in fact, whatever the programmer wants; the first element may identify a star system and the second one of the stars in the system identified by the first, for example, or the interpretation may be totally abstract, with no physical nature.)
Mutable and immutable arrays
In imperative programming languages, arrays are typically mutable by default, which means that each element of an array can be freely treated as a variable with both read and write access. In contrast, immutable arrays are sometimes encountered, arrays in which all values must be specified as soon as the array is created, and none of the elements may thereafter be modified. Immutable arrays can be used to enforce referential transparency in functional languages, but with the caveat that updating one, which really involves creating a new one that differs in only one element, requires time linear in the size of the array. Nevertheless, functional programming languages usually have support for mutable arrays. In imperative programming languages, there are often ways to create immutable arrays, should the need arise. (Java's strings are immutable by default.)
Extensible and fixed arrays
A fixed array is an array whose size cannot be changed, but is fixed at creation, whereas an extensible array is an array whose size can be changed after it is created. When the size of an array is changed from  to
to 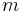 , it is understood that the first
, it is understood that the first 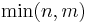 elements of the array are left intact.
elements of the array are left intact.
Fixed arrays are easy to implement. A problem with implementing extensible arrays is that we cannot always keep the array in the same place. This is because when we first allocate the array, we might not know how large it will become. We cannot allocate an unlimited amount of space for it, so instead we allocate enough space for its initial size. If the array needs to grow, then we cannot simply reserve the next memory address that the array should contain if it were larger, because this block of memory may be in use by another variable or another program. Instead, we need to allocate a new block of memory that is large enough for the extended array, and copy over all the elements. Naively, if we repeatedly extend the array one element at a time, we can force each operation to take linear time, giving 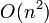 time to insert
time to insert 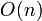 elements one at a time. This is not an acceptable performance, so another solution is to double the size of allocated memory for the array every time the array grows beyond its current memory allocation; it can be shown that insertions then take place in amortized
elements one at a time. This is not an acceptable performance, so another solution is to double the size of allocated memory for the array every time the array grows beyond its current memory allocation; it can be shown that insertions then take place in amortized  time, although some space is wasted.
time, although some space is wasted.
Array operations
Algorithms that work with arrays tend to loop over the elements of the array, considering them one (or a few) at a time. However, there are some operations that are so frequently encountered that they have library support, such as:
- Fill: Set every element in the array, or slice thereof, to the same value.
- Copy: Copies an array, or slice thereof, to another array or slice thereof, overwriting the values that were there previously, for example, setting the first, second, and third elements of an array to the values of the fifth, sixth, and seventh elements of another array, respectively.
- Search: Find the first element in the array that is equal to a given value.
- Reverse: Rearrange the elements of the array so their order is the opposite of their original order.
- Sort: Rearrange the elements of the array so that each element is less than or equal to the one following it (except the last).
- Filter: Create a new array whose elements are exactly those in an original, given array, that satisfy a given unary predicate, without rearranging them.
- Map: Apply the same unary function to every element in the array, either replacing it by the result of the function, or creating a new array that contains all the return values of the function, without rearranging them. (An example would be converting a string to uppercase.)
- Reduce: Consider each element of the array in turn, passing it to a binary function to update an accumulator, until all elements have been considered, and then return the accumulator. (Examples would be summing the array or finding its maximum element.)
Limitations
Suppose that a person cuts into line. How do we update the array of names? The problem is that everybody behind this person will have to have their IDs reassigned to reflect the new structure. That is, when we force an element into a particular location in an array, we have to shift over all the elements to its right, which requires a potentially linear amount of work copying elements. The same is true if someone in the middle of the line or the beginning leaves; all the people after him/her in the line will have to be shifted forward one position (backward in the array). When insertions and deletions are frequent, and most access is sequential, a linked list may perform better; when insertion, deletion, and random access are all frequent, the use of a tree is recommended.
Derived data structures
The array can easily be used to implement a stack, queue, deque, or binary heap.