Difference between revisions of "Optimization"
(Created page with "''This article is about improving programs. For the class of problems, see optimization problem.'' To '''optimize''' a correct program is to engineer its [[Algorithm|design ...") |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
To '''optimize''' a correct program is to engineer its [[Algorithm|design or implementation]] to improve its performance. This generally means decreasing its [[Asymptotic analysis|time complexity]], [[Asymptotic analysis|space complexity]], CPU time usage, or memory usage. Sometimes it will be possible to decrease all of these, whereas in other cases one might be sacrificed for another (especially in the so-called ''time/memory tradeoff''). Less commonly in algorithmic programming, optimization can also mean reducing disk seeks, cache faults, or response time, or increasing throughput. A specific concept that optimizes a program, such as I/O buffering, is also referred to as ''an optimization''. Generally, optimization improves the targeted performance statistic for all or almost all conceivable inputs, or the improvements it offers vastly outweigh the regressions (for example, a program may run slightly more slowly on very small inputs but significantly more quickly on medium to large inputs after optimizations have been made). It thus improves performance in both the average case and the worst case. When the average case performance is already excellent but the worst case performance needs improvement, [[randomization]] may be easier than optimization. | To '''optimize''' a correct program is to engineer its [[Algorithm|design or implementation]] to improve its performance. This generally means decreasing its [[Asymptotic analysis|time complexity]], [[Asymptotic analysis|space complexity]], CPU time usage, or memory usage. Sometimes it will be possible to decrease all of these, whereas in other cases one might be sacrificed for another (especially in the so-called ''time/memory tradeoff''). Less commonly in algorithmic programming, optimization can also mean reducing disk seeks, cache faults, or response time, or increasing throughput. A specific concept that optimizes a program, such as I/O buffering, is also referred to as ''an optimization''. Generally, optimization improves the targeted performance statistic for all or almost all conceivable inputs, or the improvements it offers vastly outweigh the regressions (for example, a program may run slightly more slowly on very small inputs but significantly more quickly on medium to large inputs after optimizations have been made). It thus improves performance in both the average case and the worst case. When the average case performance is already excellent but the worst case performance needs improvement, [[randomization]] may be easier than optimization. | ||
| + | |||
| + | For optimizations that do not affect asymptotic (scaling) behaviour, but improve time or memory usage by a constant factor only, see [[invisible constant factor]]. | ||
| + | |||
| + | ==Pruning== | ||
| + | In [[recursive]] backtracking algorithms, the central tenet of optimization is the following:<ref name="usaco">''Optimization Techniques''. USACO Training Pages, Section 4.1</ref> | ||
| + | {{ImportantConceptBox| | ||
| + | # Prune early, prune often. | ||
| + | # Don't do anything stupid. Don't do anything twice. | ||
| + | }} | ||
| + | The meaning of ''pruning'' is clear when a recursive search is depicted with a tree diagram. The solution to the problem lies on some leaf node at the very bottom of the tree. Sometimes, even though we cannot predict exactly where the solution lies in the tree, we can say for certain that it does not lie in some particular subtree. If this is the case, then there is no point in descending into that subtree at all. The decision not to descend into a subtree is called ''pruning'', because it is like cutting a branch off a real tree. This is the meaning of ''don't do anything stupid''. | ||
| + | |||
| + | Obviously, the more we prune, the smaller is the remaining part of the tree that we have to search, so the faster our algorithm is. This is the meaning of ''prune often''. | ||
| + | |||
| + | Pruning is more effective when it is done closer to the root, because it results in discarding larger subtrees. Think about how in real life, if you cut a branch close to a tree trunk, it will remove more of the tree than if you cut a branch further away. (Then remember that trees in computer science are upside-down.) This is what ''prune early'' means. | ||
| + | |||
| + | ''Don't do anything twice'' is a principle that applies whenever we have the possibility of multiple identical subtrees in a particular recursive search tree. Even if we cannot eliminate the possibility of the solution being in one of them, it is clear that we only need to search ''one'' of the multiple identical subtrees; the second time this subtree is encountered, and all subsequent times, we can simply stop searching because we know we won't find anything better than what we originally have. | ||
| + | |||
| + | ==Data structures== | ||
| + | In other types of problems, use of proper data structures can result in a significant decrease in running time. Often this can make the difference between a solution that uses <math>O(n^2)</math> time and a solution that uses <math>O(n \log n)</math> time, much better. For example: | ||
| + | * In [[selection sort]], we have to look through the entire array during each step to find the smallest element left. If we use a [[binary heap]] to efficiently look up and remove the smallest element, we obtain the much faster [[heapsort]] algorithm. | ||
| + | * The same applies in [[Dijkstra's algorithm]]. In sparse graphs, we waste too much time checking every single vertex to see whether it's the next one we should visit. Using a [[binary heap]] allows us to choose the next node much more efficiently, but in a dense graph, it simply adds overhead, and shouldn't be used. A [[Fibonacci heap]] is theoretically the best possible data structure to use for Dijkstra's algorithm in both sparse and dense graphs. | ||
| + | * Clever use of a sorted array and [[binary search]] allows us to solve the [[longest increasing subsequence]] problem in <math>O(n \log n)</math> time rather than <math>O(n^2)</math> time. | ||
| + | * If we have some dynamic set of elements and an algorithm that frequently has to check whether something belongs to this set, we can represent the set using a [[hash table]] and thus perform this check in constant time rather than linear time. | ||
| + | :* If, rather than simply failing when we cannot find the given element, we want to be able find the smallest element in the set greater than the given element, we can use an [[ordered set]] based on a [[balanced binary search tree]] or [[skip list]], rather than a hash table. This gets the job done in logarithmic time—still much better than linear. | ||
| + | * If we find ourselves having to repeatedly find the smallest element in some range of an array, any of the techniques described in the [[range minimum query]] article can speed up this section of the algorithm. | ||
| + | * If we find ourselves having to repeatedly compute some function of some range of some array whose elements may change, the [[segment tree]] can often be used to compute this function in logarithmic time rather than linear time. | ||
| + | * If we find ourselves having to repeatedly find the sum of elements in some range of an array, the [[prefix sum array]] can accomplish this in constant time when the array's elements do not change, and the [[binary indexed tree]] can accomplish it in logarithmic time if they do. Either way, it is an improvement over the naive linear-time approach of simply going through and adding all the elements up individually. | ||
| + | * If we have some given set of strings and we find ourselves repeatedly having to check whether strings belong to our set, we can use a [[trie]] to accomplish each of these lookups in linear time, rather than having to compare the string to everything that's already in the set individually. | ||
| + | * In some rare cases, such as {{Problem|coci081p5|Skakavac}}, you will have to design your own data structure, rather than using a standard one out of an algorithms text. Not using any data structure will give you an <math>O(n^3)</math> solution, and using a [[binary indexed tree]] gives <math>O(n^2 \log n)</math> time complexity but also <math>O(n^2)</math> extra memory usage. The model solution uses a custom data structure that cuts down the extra memory usage to <math>O(n)</math>, which is small enough to get full marks. | ||
| + | |||
| + | ==References== | ||
| + | <references/> | ||
Latest revision as of 01:34, 5 January 2012
This article is about improving programs. For the class of problems, see optimization problem.
To optimize a correct program is to engineer its design or implementation to improve its performance. This generally means decreasing its time complexity, space complexity, CPU time usage, or memory usage. Sometimes it will be possible to decrease all of these, whereas in other cases one might be sacrificed for another (especially in the so-called time/memory tradeoff). Less commonly in algorithmic programming, optimization can also mean reducing disk seeks, cache faults, or response time, or increasing throughput. A specific concept that optimizes a program, such as I/O buffering, is also referred to as an optimization. Generally, optimization improves the targeted performance statistic for all or almost all conceivable inputs, or the improvements it offers vastly outweigh the regressions (for example, a program may run slightly more slowly on very small inputs but significantly more quickly on medium to large inputs after optimizations have been made). It thus improves performance in both the average case and the worst case. When the average case performance is already excellent but the worst case performance needs improvement, randomization may be easier than optimization.
For optimizations that do not affect asymptotic (scaling) behaviour, but improve time or memory usage by a constant factor only, see invisible constant factor.
Pruning[edit]
In recursive backtracking algorithms, the central tenet of optimization is the following:[1]
- Prune early, prune often.
- Don't do anything stupid. Don't do anything twice.
The meaning of pruning is clear when a recursive search is depicted with a tree diagram. The solution to the problem lies on some leaf node at the very bottom of the tree. Sometimes, even though we cannot predict exactly where the solution lies in the tree, we can say for certain that it does not lie in some particular subtree. If this is the case, then there is no point in descending into that subtree at all. The decision not to descend into a subtree is called pruning, because it is like cutting a branch off a real tree. This is the meaning of don't do anything stupid.
Obviously, the more we prune, the smaller is the remaining part of the tree that we have to search, so the faster our algorithm is. This is the meaning of prune often.
Pruning is more effective when it is done closer to the root, because it results in discarding larger subtrees. Think about how in real life, if you cut a branch close to a tree trunk, it will remove more of the tree than if you cut a branch further away. (Then remember that trees in computer science are upside-down.) This is what prune early means.
Don't do anything twice is a principle that applies whenever we have the possibility of multiple identical subtrees in a particular recursive search tree. Even if we cannot eliminate the possibility of the solution being in one of them, it is clear that we only need to search one of the multiple identical subtrees; the second time this subtree is encountered, and all subsequent times, we can simply stop searching because we know we won't find anything better than what we originally have.
Data structures[edit]
In other types of problems, use of proper data structures can result in a significant decrease in running time. Often this can make the difference between a solution that uses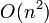 
time and a solution that uses 
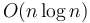time, much better. For example:
- In selection sort, we have to look through the entire array during each step to find the smallest element left. If we use a binary heap to efficiently look up and remove the smallest element, we obtain the much faster heapsort algorithm.
- The same applies in Dijkstra's algorithm. In sparse graphs, we waste too much time checking every single vertex to see whether it's the next one we should visit. Using a binary heap allows us to choose the next node much more efficiently, but in a dense graph, it simply adds overhead, and shouldn't be used. A Fibonacci heap is theoretically the best possible data structure to use for Dijkstra's algorithm in both sparse and dense graphs.
- Clever use of a sorted array and binary search allows us to solve the longest increasing subsequence problem in 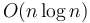time rather than 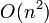time.
- If we have some dynamic set of elements and an algorithm that frequently has to check whether something belongs to this set, we can represent the set using a hash table and thus perform this check in constant time rather than linear time.
- If, rather than simply failing when we cannot find the given element, we want to be able find the smallest element in the set greater than the given element, we can use an ordered set based on a balanced binary search tree or skip list, rather than a hash table. This gets the job done in logarithmic time—still much better than linear.
- If we find ourselves having to repeatedly find the smallest element in some range of an array, any of the techniques described in the range minimum query article can speed up this section of the algorithm.
- If we find ourselves having to repeatedly compute some function of some range of some array whose elements may change, the segment tree can often be used to compute this function in logarithmic time rather than linear time.
- If we find ourselves having to repeatedly find the sum of elements in some range of an array, the prefix sum array can accomplish this in constant time when the array's elements do not change, and the binary indexed tree can accomplish it in logarithmic time if they do. Either way, it is an improvement over the naive linear-time approach of simply going through and adding all the elements up individually.
- If we have some given set of strings and we find ourselves repeatedly having to check whether strings belong to our set, we can use a trie to accomplish each of these lookups in linear time, rather than having to compare the string to everything that's already in the set individually.
- In some rare cases, such as Skakavac, you will have to design your own data structure, rather than using a standard one out of an algorithms text. Not using any data structure will give you an
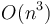solution, and using a binary indexed tree gives 
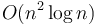time complexity but also 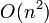extra memory usage. The model solution uses a custom data structure that cuts down the extra memory usage to 
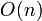, which is small enough to get full marks.
References[edit]
- ↑ Optimization Techniques. USACO Training Pages, Section 4.1
