Difference between revisions of "Half-open interval"
| Line 5: | Line 5: | ||
* The interval of length <math>n</math> starting at <math>i</math> can simply be denoted <math>[i,i+n)</math>, rather than the more cumbersome <math>[i,i+n-1]</math>. | * The interval of length <math>n</math> starting at <math>i</math> can simply be denoted <math>[i,i+n)</math>, rather than the more cumbersome <math>[i,i+n-1]</math>. | ||
* The ''disjoint'' union of <math>[i,j)</math> and <math>[j,k)</math> is <math>[i,k)</math>; and likewise any left half-open interval <math>[a,b)</math> may be divided by intermediate values <math>a < c_0 < c_1 < ... < c_n < b</math> into a disjoint union of left half-open intervals <math>[a,c_0) \cup [c_0,c_1) \cup [c_1,c_2) \cup ... \cup [c_n, b)</math>; ''i.e.'', endpoints telescope nicely with half-open intervals, whereas they do not with fully open or fully closed intervals. | * The ''disjoint'' union of <math>[i,j)</math> and <math>[j,k)</math> is <math>[i,k)</math>; and likewise any left half-open interval <math>[a,b)</math> may be divided by intermediate values <math>a < c_0 < c_1 < ... < c_n < b</math> into a disjoint union of left half-open intervals <math>[a,c_0) \cup [c_0,c_1) \cup [c_1,c_2) \cup ... \cup [c_n, b)</math>; ''i.e.'', endpoints telescope nicely with half-open intervals, whereas they do not with fully open or fully closed intervals. | ||
| + | * See also [[prefix sum array and difference array]]. | ||
Here is an example of when left half-open intervals may be useful. We usually think of one-dimensional [[array]]s as being lines of boxes, where each box represents an element. Sometimes, we want to use a one-dimensional array to store some information about exact points in time; maybe something happens exactly at ''t'' = 15 s and ends exactly at ''t'' = 21 s. A second is an interval delineated by two points (that are, by definition, one second apart); a second is like a box, but a point in time is like one of the lines that separates two boxes. We can represent the interval in time between 15 s and 21 s as the half-open interval [15, 21); that is, identify each box in the array with the point of time when it ''starts''. Since the last second of the event is between 20 s and 21 s (instead of 21 s and 22 s), the box at index 21 is not used. | Here is an example of when left half-open intervals may be useful. We usually think of one-dimensional [[array]]s as being lines of boxes, where each box represents an element. Sometimes, we want to use a one-dimensional array to store some information about exact points in time; maybe something happens exactly at ''t'' = 15 s and ends exactly at ''t'' = 21 s. A second is an interval delineated by two points (that are, by definition, one second apart); a second is like a box, but a point in time is like one of the lines that separates two boxes. We can represent the interval in time between 15 s and 21 s as the half-open interval [15, 21); that is, identify each box in the array with the point of time when it ''starts''. Since the last second of the event is between 20 s and 21 s (instead of 21 s and 22 s), the box at index 21 is not used. | ||
The choice of left half-open intervals over right half-open intervals is arbitrary, but appears to be a ''de facto'' standard. | The choice of left half-open intervals over right half-open intervals is arbitrary, but appears to be a ''de facto'' standard. | ||
Revision as of 08:11, 15 December 2011
A left half-open interval is an interval of the form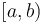 
; it contains all 
such that 
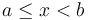. It is often useful to express problems, algorithms, data structures, and library functions in terms of left half-open intervals of integers; a segment of an array is then specified by giving the left endpoint, that is, the index to the first element in the segment, and the right endpoint, which is the element just after the last element in the segment. For example, in C++, to sort a segment of an array A from the third element to the sixth element, inclusive, the code is std::sort(A+3, A+7);. The STL containers std::vector, std::list, std::deque, std::set, and std::map all have two member functions, begin() and end(), where the latter returns an iterator, not to the actual last element in the container, but to an imaginary element "just past the end".
Left half-open intervals are convenient because they have the following desirable properties:
- The interval 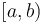contains
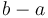elements exactly (rather than 
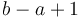or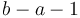 
). - The interval of length
starting at 
can simply be denoted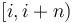 
, rather than the more cumbersome ![[i,i+n-1]](/wiki/images/math/c/c/0/cc05e03233e068c37257abd8e22d3126.png)
. - The disjoint union of
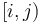and 
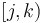is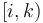 
; and likewise any left half-open interval 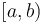may be divided by intermediate values 
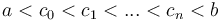into a disjoint union of left half-open intervals 
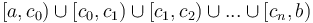; i.e., endpoints telescope nicely with half-open intervals, whereas they do not with fully open or fully closed intervals. - See also prefix sum array and difference array.
Here is an example of when left half-open intervals may be useful. We usually think of one-dimensional arrays as being lines of boxes, where each box represents an element. Sometimes, we want to use a one-dimensional array to store some information about exact points in time; maybe something happens exactly at t = 15 s and ends exactly at t = 21 s. A second is an interval delineated by two points (that are, by definition, one second apart); a second is like a box, but a point in time is like one of the lines that separates two boxes. We can represent the interval in time between 15 s and 21 s as the half-open interval [15, 21); that is, identify each box in the array with the point of time when it starts. Since the last second of the event is between 20 s and 21 s (instead of 21 s and 22 s), the box at index 21 is not used.
The choice of left half-open intervals over right half-open intervals is arbitrary, but appears to be a de facto standard.
