Half-open interval
A right half-open interval (less commonly left half-closed interval) is an interval of the form 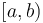 ; it contains all
; it contains all  such that
such that 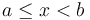 . It is often useful to express problems, algorithms, data structures, and library functions in terms of right half-open intervals of integers; a segment of an array is then specified by giving the left endpoint, that is, the index to the first element in the segment, and the right endpoint, which is the element just after the last element in the segment. For example, in C++, to sort a segment of an array
. It is often useful to express problems, algorithms, data structures, and library functions in terms of right half-open intervals of integers; a segment of an array is then specified by giving the left endpoint, that is, the index to the first element in the segment, and the right endpoint, which is the element just after the last element in the segment. For example, in C++, to sort a segment of an array A from the third element to the sixth element, inclusive, the code is std::sort(A+3, A+7);. The STL containers std::vector, std::list, std::deque, std::set, and std::map all have two member functions, begin() and end(), where the latter returns an iterator, not to the actual last element in the container, but to an imaginary element "just past the end".
Right half-open intervals are convenient because they have the following desirable properties:
- The interval
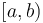 contains
contains 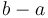 elements exactly (rather than
elements exactly (rather than 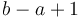 or
or 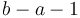 ).
). - The interval of length
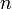 starting at
starting at 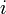 can simply be denoted
can simply be denoted 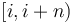 , rather than the more cumbersome
, rather than the more cumbersome ![[i,i+n-1]](/wiki/images/math/c/c/0/cc05e03233e068c37257abd8e22d3126.png) .
. - The disjoint union of
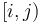 and
and 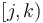 is
is 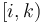 ; and likewise any right half-open interval
; and likewise any right half-open interval 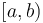 may be divided by intermediate values
may be divided by intermediate values 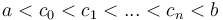 into a disjoint union of right half-open intervals
into a disjoint union of right half-open intervals 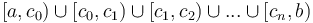 ; i.e., endpoints telescope nicely with half-open intervals, whereas they do not with fully open or fully closed intervals.
; i.e., endpoints telescope nicely with half-open intervals, whereas they do not with fully open or fully closed intervals. - See also prefix sum array and difference array.
Here is an example of when right half-open intervals may be useful. We usually think of one-dimensional arrays as being lines of boxes, where each box represents an element. Sometimes, we want to use a one-dimensional array to store some information about exact points in time; maybe something happens exactly at t = 15 s and ends exactly at t = 21 s. A second is an interval delineated by two points (that are, by definition, one second apart); a second is like a box, but a point in time is like one of the lines that separates two boxes. We can represent the interval in time between 15 s and 21 s as the half-open interval [15, 21); that is, identify each box in the array with the point of time when it starts. Since the last second of the event is between 20 s and 21 s (instead of 21 s and 22 s), the box at index 21 is not used.
The choice of right half-open intervals over left half-open intervals is arbitrary, but appears to be a de facto standard.