Difference between revisions of "Shortest path"
(Created page with "The '''shortest paths''' problem is one of the most fundamental problems in graph theory. Given a directed graph <math>G = (V,E)</math>, possibly weighted, and a set of pairs...") |
(→All-pairs shortest paths) |
||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | The '''shortest paths''' problem is one of the most fundamental problems in [[graph theory]]. Given a directed graph <math>G = (V,E)</math>, possibly weighted, and a set of pairs of vertices <math>\{(u_1,v_1), ..., (u_n,v_n)\}, u_i, v_i \in V</math>, the problem is to compute, for each <math>i</math>, a path in <math>G</math> from <math>u_i</math> to <math>v_i</math> (a list of vertices <math>u_i = s_{i,0}, s_{i,1}, ..., s_{i,k} = v_i</math> such that for all <math>0 \leq j < k</math>, <math>(s_{i,j},s_{i,j+1}) \in E</math>) such that no other path in <math>G</math> from <math>u_i</math> to <math>v_i</math> has a lower total weight. | + | The '''shortest paths''' problem is one of the most fundamental problems in [[graph theory]]. Given a directed graph <math>G = (V,E)</math>, possibly weighted, and a set of pairs of vertices <math>\{(u_1,v_1), ..., (u_n,v_n)\}, u_i, v_i \in V</math>, the problem is to compute, for each <math>i</math>, a '''simple''' path in <math>G</math> from <math>u_i</math> to <math>v_i</math> (a list of vertices <math>u_i = s_{i,0}, s_{i,1}, ..., s_{i,k} = v_i</math> such that for all <math>0 \leq j < k</math>, <math>(s_{i,j},s_{i,j+1}) \in E</math>) such that no other simple path in <math>G</math> from <math>u_i</math> to <math>v_i</math> has a lower total weight. |
Shortest paths in undirected graphs can be computed by replacing each undirected edge with two arcs of the same weight, one going in each direction, to obtain a directed graph. | Shortest paths in undirected graphs can be computed by replacing each undirected edge with two arcs of the same weight, one going in each direction, to obtain a directed graph. | ||
| + | |||
| + | '''Theorem''': In a graph with no cycles of negative weight, the shortest path is no shorter than the shortest simple path. (On the other hand, in a graph with a negative-weight cycle, lengths of paths may be unbounded below.) | ||
| + | |||
| + | '''Proof''': We show that any path from <math>u</math> to <math>v</math> can be transformed into a simple path from <math>u</math> to <math>v</math> which is at least as short. Let the path be denoted <math>[u = s_0, s_1, ..., s_j = v]</math>. We proceed by induction on the number of pairs <math>(i,j)</math> (with <math>i \neq j</math>) such that <math>s_i = s_j</math>, which is countable. When there are zero such pairs, the path is already simple, and nothing needs to be done. Otherwise, we transform the path into another path with fewer such pairs but equal or lesser weight by removing the vertices <math>s_i, s_{i+1}, ..., s_{j-1}</math> from the path. The weight of the path therefore decreases by an amount equal to the weight of the cycle <math>s_i, s_{i+1}, ..., s_j = s_i</math>, which is nonnegative. <math>_\blacksquare</math> | ||
| + | |||
| + | '''Corollary''': Assuming our graphs have no cycles of negative weight, the restriction that the shortest paths be simple is immaterial. Therefore, we will assume in the foregoing discussion that our graphs have no cycles of negative weight, for the problem of finding shortest ''simple'' paths in graphs containing negative-weight cycles is NP-complete. | ||
| + | |||
| + | '''Corollary''': In a finite connected graph, a shortest path always exists. (To prove this we simply use the fact that the graph has a finite number of simple paths, and only simple paths need be considered. So one of them must be the shortest.) | ||
==Variations== | ==Variations== | ||
| Line 8: | Line 16: | ||
* In the ''single-source shortest paths'' problem, the problem set is of the form <math>\{u\} \times V</math>. One vertex, <math>u</math>, is designated the ''source'', and we wish to find the shortest paths from the source to all other vertices. (To solve the analogous ''single-destination shortest paths'' problem, we merely reverse the directions of all edges, which reduces it to single-source.) | * In the ''single-source shortest paths'' problem, the problem set is of the form <math>\{u\} \times V</math>. One vertex, <math>u</math>, is designated the ''source'', and we wish to find the shortest paths from the source to all other vertices. (To solve the analogous ''single-destination shortest paths'' problem, we merely reverse the directions of all edges, which reduces it to single-source.) | ||
* In the ''all-pairs shortest paths'' problem, the problem set is <math>V \times V</math>; that is, we wish to know the shortest paths from every vertex to every other vertex. | * In the ''all-pairs shortest paths'' problem, the problem set is <math>V \times V</math>; that is, we wish to know the shortest paths from every vertex to every other vertex. | ||
| + | |||
| + | ==Approach== | ||
| + | All the shortest paths algorithms discussed in this article have the same basic approach. At their core, they compute not the shortest paths themselves, but the distances. Using information computed in order to compute the distances, one can easily then reconstruct the paths themselves. They begin with the knowledge that the distance from any vertex to itself is zero, and they overestimate all other distances they need. (By this it is meant that they find a number <math>d_{i,j}</math> for each pair <math>(i,j)</math> under consideration such that the distance from <math>i</math> to <math>j</math> is less than or equal to <math>d_{i,j}</math>.) If <math>(i,j) \in E</math>, then the initial overestimate for the distance from <math>i</math> to <math>j</math> is the weight of the edge <math>(i,j)</math>; otherwise it is infinite. At some point, all overestimates will be refined, perhaps gradually, perhaps at once, so that once the algorithm has terminated, they are exactly the correct distances. | ||
| + | |||
| + | ===Relaxation=== | ||
| + | There are theoretically many ways to refine overestimates but a specific way, known as '''relaxation''', is used in all the algorithms discussed in this article. Relaxation can take place when three conditions are met: | ||
| + | # The currently best overestimate for the distance from some vertex <math>i</math> to some vertex <math>k</math> is <math>d_1</math>; | ||
| + | # The currently best overestimate for the distance from <math>k</math> to some vertex <math>j</math> is <math>d_2</math>, | ||
| + | # The currently best overestimate for the distance from <math>i</math> to <math>j</math> is greater than <math>d_1+d_2</math>. (This includes the case in which it is infinite.) | ||
| + | Relaxation refines the best overestimate for the distance from <math>i</math> to <math>j</math> by setting it to <math>d_1+d_2</math>, which is better than its current value. | ||
| + | <!-- | ||
| + | '''Theorem''': Relaxation will never strictly underestimate the distance from <math>i</math> to <math>j</math>. | ||
| + | |||
| + | '''Proof''': Concatenating the shortest paths from <math>i</math> to <math>k</math> and <math>k</math> to <math>j</math> gives a path from <math>i</math> to <math>j</math> with length less than or equal to <math>d_1+d_2</math>. Therefore <math>d_1+d_2</math> is an overestimate. <math>_\blacksquare</math> | ||
| + | |||
| + | '''Theorem''': Relaxation is impossible when all distances under consideration are correctly known. | ||
| + | |||
| + | '''Proof''': Using the variables defined above, this implies that the distance from <math>i</math> to <math>j</math> is in fact greater than the sum of the distances from <math>i</math> to <math>k</math> and <math>k</math> to <math>j</math>, which is impossible, as we can merely concatenate shortest paths from <math>i</math> to <math>k</math> and <math>k</math> to <math>j</math> to obtain a path from <math>i</math> to <math>j</math> of <math>d_1+d_2</math>, which is less. <math>_\blacksquare</math> | ||
| + | |||
| + | '''Theorem''': In a graph with a finite number of vertices, only a finite number of successive relaxations can take place, assuming the initial conditions are as defined above. | ||
| + | |||
| + | '''Proof''': We show by induction on the number of relaxations so far performed that if the current best overestimate on the distance from <math>i \in V</math> to <math>j \in V</math> is finite and equals <math>d</math>, then we can exhibit a path of weight <math>d</math> from <math>i</math> to <math>j</math>. Clearly this is true initially, when no relaxations have been performed, because we used empty paths and paths consisting of only one edge to set the initial overestimates. The inductive step is also obvious, because we can concatenate the already-known paths of length <math>d_1</math> and <math>d_2</math> from <math>i</math> to <math>k</math> and <math>k</math> to <math>j</math>, respectively, to obtain a path of length <math>d_1+d_2</math> from <math>i</math> to <math>j</math>. | ||
| + | |||
| + | After a relaxation takes place, the path we have from <math>i</math> to <math>j</math> contains at least as many edges as the paths we have from <math>i</math> to <math>k</math> and from <math>k</math> to <math>j</math>. Now, at most a finite number of relaxations | ||
| + | --> | ||
| + | |||
| + | '''Theorem''': When the distances from <math>u</math> to all other vertices are all overestimated, but no relaxations are possible, then those distances are all known correctly. Contrapositively, if at there exists <math>v \in V</math> such that the distance from <math>u</math> to <math>v</math> is not correctly known, then relaxation must be possible somewhere in the graph. | ||
| + | |||
| + | '''Proof''': By induction on the number of edges in some shortest path from <math>u</math> to <math>v</math> (which we can take to be simple). It is vacuously true when this is zero or one, because all paths of length zero or one were accounted for in the initial overestimates. Assume the path has at least two edges, and denote by <math>s</math> the last vertex on the path before <math>v</math>. If the distance from <math>u</math> to <math>s</math> or from <math>s</math> to <math>v</math> is not known, then by the inductive hypothesis, we are done. Otherwise, notice that the path contains two subpaths, one from <math>u</math> to <math>s</math> and one from <math>s</math> to <math>v</math> (the latter is trivial as it consists of a single edge), and that each of these must itself be a shortest path, otherwise we could replace it with a shorter path to obtain a shorter path from <math>u</math> to <math>v</math>, a contradiction. Now, as the distances from <math>u</math> to <math>s</math> and <math>s</math> to <math>v</math> are correctly known, and the correct distance from <math>u</math> to <math>v</math> is exactly the sum of the distances from <math>u</math> to <math>s</math> and <math>s</math> to <math>v</math> (as these values equal the weights of the aforementioned subpaths), and our overestimate of the distance from <math>u</math> to <math>v</math> is incorrect, it must be strictly greater than the sum of the distances from <math>u</math> to <math>s</math> and <math>s</math> to <math>v</math>. Hence <math>(u,v)</math> can be relaxed. <math>_\blacksquare</math> | ||
==Single-source shortest paths== | ==Single-source shortest paths== | ||
| + | In an unweighted graph, the single-source shortest paths may be determined by performing [[breadth-first search]] from the source. This is correct by definition; breadth-first search visits nodes in increasing order of their distance from the start node, so that as soon as we visit a node, we immediately know the correct distance to this node. This is guaranteed to terminate after considering each edge at most twice (once from each end in an undirected graph), since we do not expand from nodes that have already been visited. It follows that the running time is <math>O(E+V)</math>. BFS also solves the problem when some edges are allowed to have weight zero (by using a [[deque]] in place of the [[queue]]). | ||
| + | |||
| + | In a weighted graph with nonnegative weights, it is still possible to visit the vertices in increasing order of distance from the source. This is because the source is obviously the closest to itself, the next closest vertex is obviously one of its immediate neighbors, the next closest is obviously either another immediate neighbor of the source or an immediate neighbor of the second closest vertex, and so on --- the length of a path cannot decrease as more nodes are added to the end of it. So by replacing the queue with a [[priority queue]] and greedily picking the next vertex to visit, we obtain [[Dijkstra's algorithm]], which is slower by only a log factor due to the priority queue, <math>O((E+V)\log V)</math> overall in a finite graph. (In a dense graph, it is also possible to implement this in <math>O(E+V^2)</math> time, which is asymptotically optimal in this case.) | ||
| + | |||
| + | If, on the other hand, edges of negative weight exist, but not in a way that introduces negative-weight cycles, there is still a simple way to find shortest paths, known as the [[Bellman–Ford algorithm]]. This works by repeatedly trying to relax each edge in the graph; it is not too hard to show that after doing this enough times, the correct shortest paths will all be known. Specifically, <math>V-1</math> iterations are required, so the running time is <math>O(VE)</math>. Another solution, which is sometimes faster, is the [[Shortest Path Faster Algorithm]] (SPFA). | ||
==All-pairs shortest paths== | ==All-pairs shortest paths== | ||
| + | We might try to find all-pairs shortest paths by running a single-source shortest paths algorithm using each vertex in turn as the source. Hence, we have the following bounds with a [[binary heap]] implementation of the [[priority queue]] ADT: | ||
| + | * <math>O(V(E+V))</math> when the graph is unweighted | ||
| + | * <math>O(V(E+V)\log V)</math> when the edge weights are nonnegative and the graph is sparse (<math>O(V(E + \log V))</math> using a [[Fibonacci heap]]) | ||
| + | * <math>O(VE+V^3)</math> when the edge weights are nonnegative and the graph is dense | ||
| + | * <math>O(V^2E)</math> when edge weights are allowed to be negative, but no negative-weight cycles exist. | ||
| + | |||
| + | There is also a general-purpose technique called the [[Floyd–Warshall]] algorithm, which is often considered [[Dynamic programming|dynamic]], that solves all four cases in <math>O(V^3)</math> time. It works by using each vertex in turn and using it to try to relax the distance between every pair of nodes in the graph. When the graph is dense, Floyd–Warshall is just as fast as BFS or Dijkstra's, and it always outperforms Bellman–Ford. So we have the bound <math>O(V(E+V)\log V)</math> for sparse graphs with nonnegative edge weights and <math>O(V^3)</math> for dense graphs. | ||
| + | |||
| + | What if the graph is sparse and it has negative edge weights? Can we do better than <math>O(V^3)</math> here? Not using the Bellman–Ford algorithm <math>V</math> times, certainly. However, it turns out that it is possible to run Bellman–Ford ''once'' and thus transform the graph into a form in which all edge weights are nonnegative, then run Dijkstra's <math>V</math> times. This gives a method known as [[Johnson's algorithm]] that matches the time bound for graphs with nonnegative edge weights (since the time taken to run Bellman–Ford is asymptotically dominated by the time taken to run <math>V</math> invocations of Dijkstra's). | ||
==Single-pair shortest path== | ==Single-pair shortest path== | ||
| + | We can compute a single-pair shortest path by taking the source <math>s</math> and running single-source shortest paths from it, and simply extracting the shortest path to the destination <math>t</math>. This computes a lot of extra information (namely, the shortest paths to all the other vertices as well), so we might wonder whether it is possible to do better. It turns out that there are no known single-pair shortest path algorithms that outperform single-source shortest paths algorithms ''in the worst case''. Nevertheless, it is often possible to do better in the ''average case''. | ||
| + | |||
| + | (Note: if edges of negative weight are allowed to exist in an infinite graph, then the problem is impossible; if any bound on the running time to find a shortest path is claimed, we can defeat this claim by constructing a graph in which the shortest path involves a highly negatively weighted edge that is extremely far away, too far to be explored within the time bound.) | ||
| + | |||
| + | ===A* or heuristic search=== | ||
| + | In the single-pair shortest path problem, we know exactly where we want to go, we just don't know how to get there. But what if we were able to guess roughly how far away we are from the destination? Then we could proceed as in Dijkstra's algorithm, but give priority to exploring edges that we think take us closer to the destination rather than further away. Formally, we define a ''heuristic function'' <math>h:V \to \mathbb{R}</math> such that <math>h(v)</math> is a "guess" for the actual distance between <math>v</math> and <math>t</math> (the destination). If we can find such a heuristic function that never ''overestimates'' (only underestimates) the correct distance, we can use the [[A* search algorithm]] to take advantage of this information to help find a shortest path more quickly. (If <math>h</math> overestimates, then we may still get a relatively short path, but we are not guaranteed that it is a correct shortest path.) The better our estimates with <math>h</math>, the faster the search, but in the worst case, in which our heuristic is totally off, we cannot improve much over Dijkstra's. | ||
| + | |||
| + | ===Meet-in-the-middle=== | ||
| + | Another example of when we don't have to worry much about the worst case, and hence might be able to get a better search time, is when the graph we are searching is extremely large but yet we know that the shortest path is relatively short. For example, consider the Rubik's cube graph, in which each legal position is a vertex and an edge exists between two vertices if the positions they represent can be interconverted with one face turn. There are approximately <math>4.3\times10^{19}</math> positions of the Rubik's cube, but the shortest path between any pair of vertices always has length 20 or less.<ref>Tomas Rokicki ''et al.'' "God's Number is 20". Retrieved 2011-03-02 from http://cube20.org/</ref> The graph we are searching may even be infinite. | ||
| + | |||
| + | Meet-in-the-middle search works similarly to a single-source search such as BFS or Djikstra's algorithm, but it differs in that the algorithm branches outward from both the source and the destination (''backward'' along directed edges, if any). In this way we simultaneously build the beginning of the path (by searching from the source) and the end (by searching from the destination). When a common vertex is reached, these two pieces of the path may be assembled to form the full path. To understand why this is faster, imagine we were to execute BFS on the Rubik's Cube graph in order to try to find a path from a scrambled position to the solved position. Each vertex in the graph has degree 18 (three possible moves per face), so, if the distance from the scrambled position to the solved position is, say, 8, we will visit on the order of 18<sup>8</sup> vertices in the search (about 11 billion). If on the other hand we found this path by finding a path of length 4 from the source and a path of length 4 from the destination that happened to share an endpoint, we would only visit on the order of 2×18<sup>4</sup> vertices, which is about 210000. So we have cut down the size of the part of the graph we have to explore by a factor of about 50000. Note however that there is no free lunch; we need some way of determining when a vertex has been visited both forward and backward, such as a hash table. | ||
==References== | ==References== | ||
| + | <references/> | ||
Latest revision as of 07:09, 26 May 2011
The shortest paths problem is one of the most fundamental problems in graph theory. Given a directed graph 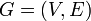 , possibly weighted, and a set of pairs of vertices
, possibly weighted, and a set of pairs of vertices 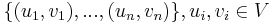 , the problem is to compute, for each
, the problem is to compute, for each  , a simple path in
, a simple path in  from
from 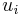 to
to 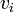 (a list of vertices
(a list of vertices 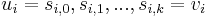 such that for all
such that for all 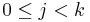 ,
, 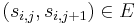 ) such that no other simple path in
) such that no other simple path in  from
from 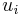 to
to 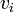 has a lower total weight.
has a lower total weight.
Shortest paths in undirected graphs can be computed by replacing each undirected edge with two arcs of the same weight, one going in each direction, to obtain a directed graph.
Theorem: In a graph with no cycles of negative weight, the shortest path is no shorter than the shortest simple path. (On the other hand, in a graph with a negative-weight cycle, lengths of paths may be unbounded below.)
Proof: We show that any path from  to
to  can be transformed into a simple path from
can be transformed into a simple path from  to
to  which is at least as short. Let the path be denoted
which is at least as short. Let the path be denoted ![[u = s_0, s_1, ..., s_j = v]](/wiki/images/math/6/8/6/686eea80a554ea2def3daa7aae0e81d4.png) . We proceed by induction on the number of pairs
. We proceed by induction on the number of pairs 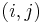 (with
(with 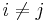 ) such that
) such that 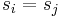 , which is countable. When there are zero such pairs, the path is already simple, and nothing needs to be done. Otherwise, we transform the path into another path with fewer such pairs but equal or lesser weight by removing the vertices
, which is countable. When there are zero such pairs, the path is already simple, and nothing needs to be done. Otherwise, we transform the path into another path with fewer such pairs but equal or lesser weight by removing the vertices 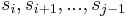 from the path. The weight of the path therefore decreases by an amount equal to the weight of the cycle
from the path. The weight of the path therefore decreases by an amount equal to the weight of the cycle  , which is nonnegative.
, which is nonnegative. 
Corollary: Assuming our graphs have no cycles of negative weight, the restriction that the shortest paths be simple is immaterial. Therefore, we will assume in the foregoing discussion that our graphs have no cycles of negative weight, for the problem of finding shortest simple paths in graphs containing negative-weight cycles is NP-complete.
Corollary: In a finite connected graph, a shortest path always exists. (To prove this we simply use the fact that the graph has a finite number of simple paths, and only simple paths need be considered. So one of them must be the shortest.)
Contents
Variations[edit]
Three variations of the shortest path algorithm exist, and they are discussed in the following sections.
- In the single-pair shortest path problem, there is only one pair
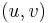 in the problem set. In other words the shortest path is desired between a single pair of vertices.
in the problem set. In other words the shortest path is desired between a single pair of vertices. - In the single-source shortest paths problem, the problem set is of the form
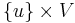 . One vertex,
. One vertex,  , is designated the source, and we wish to find the shortest paths from the source to all other vertices. (To solve the analogous single-destination shortest paths problem, we merely reverse the directions of all edges, which reduces it to single-source.)
, is designated the source, and we wish to find the shortest paths from the source to all other vertices. (To solve the analogous single-destination shortest paths problem, we merely reverse the directions of all edges, which reduces it to single-source.) - In the all-pairs shortest paths problem, the problem set is
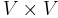 ; that is, we wish to know the shortest paths from every vertex to every other vertex.
; that is, we wish to know the shortest paths from every vertex to every other vertex.
Approach[edit]
All the shortest paths algorithms discussed in this article have the same basic approach. At their core, they compute not the shortest paths themselves, but the distances. Using information computed in order to compute the distances, one can easily then reconstruct the paths themselves. They begin with the knowledge that the distance from any vertex to itself is zero, and they overestimate all other distances they need. (By this it is meant that they find a number 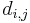 for each pair
for each pair 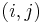 under consideration such that the distance from
under consideration such that the distance from  to
to  is less than or equal to
is less than or equal to 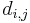 .) If
.) If 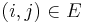 , then the initial overestimate for the distance from
, then the initial overestimate for the distance from  to
to  is the weight of the edge
is the weight of the edge 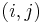 ; otherwise it is infinite. At some point, all overestimates will be refined, perhaps gradually, perhaps at once, so that once the algorithm has terminated, they are exactly the correct distances.
; otherwise it is infinite. At some point, all overestimates will be refined, perhaps gradually, perhaps at once, so that once the algorithm has terminated, they are exactly the correct distances.
Relaxation[edit]
There are theoretically many ways to refine overestimates but a specific way, known as relaxation, is used in all the algorithms discussed in this article. Relaxation can take place when three conditions are met:
- The currently best overestimate for the distance from some vertex
 to some vertex
to some vertex  is
is 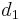 ;
; - The currently best overestimate for the distance from
 to some vertex
to some vertex  is
is 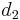 ,
, - The currently best overestimate for the distance from
 to
to  is greater than
is greater than 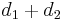 . (This includes the case in which it is infinite.)
. (This includes the case in which it is infinite.)
Relaxation refines the best overestimate for the distance from  to
to  by setting it to
by setting it to 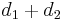 , which is better than its current value.
, which is better than its current value.
Theorem: When the distances from  to all other vertices are all overestimated, but no relaxations are possible, then those distances are all known correctly. Contrapositively, if at there exists
to all other vertices are all overestimated, but no relaxations are possible, then those distances are all known correctly. Contrapositively, if at there exists 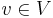 such that the distance from
such that the distance from  to
to  is not correctly known, then relaxation must be possible somewhere in the graph.
is not correctly known, then relaxation must be possible somewhere in the graph.
Proof: By induction on the number of edges in some shortest path from  to
to  (which we can take to be simple). It is vacuously true when this is zero or one, because all paths of length zero or one were accounted for in the initial overestimates. Assume the path has at least two edges, and denote by
(which we can take to be simple). It is vacuously true when this is zero or one, because all paths of length zero or one were accounted for in the initial overestimates. Assume the path has at least two edges, and denote by  the last vertex on the path before
the last vertex on the path before  . If the distance from
. If the distance from  to
to  or from
or from  to
to  is not known, then by the inductive hypothesis, we are done. Otherwise, notice that the path contains two subpaths, one from
is not known, then by the inductive hypothesis, we are done. Otherwise, notice that the path contains two subpaths, one from  to
to  and one from
and one from  to
to  (the latter is trivial as it consists of a single edge), and that each of these must itself be a shortest path, otherwise we could replace it with a shorter path to obtain a shorter path from
(the latter is trivial as it consists of a single edge), and that each of these must itself be a shortest path, otherwise we could replace it with a shorter path to obtain a shorter path from  to
to  , a contradiction. Now, as the distances from
, a contradiction. Now, as the distances from  to
to  and
and  to
to  are correctly known, and the correct distance from
are correctly known, and the correct distance from  to
to  is exactly the sum of the distances from
is exactly the sum of the distances from  to
to  and
and  to
to  (as these values equal the weights of the aforementioned subpaths), and our overestimate of the distance from
(as these values equal the weights of the aforementioned subpaths), and our overestimate of the distance from  to
to  is incorrect, it must be strictly greater than the sum of the distances from
is incorrect, it must be strictly greater than the sum of the distances from  to
to  and
and  to
to  . Hence
. Hence 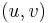 can be relaxed.
can be relaxed. 
Single-source shortest paths[edit]
In an unweighted graph, the single-source shortest paths may be determined by performing breadth-first search from the source. This is correct by definition; breadth-first search visits nodes in increasing order of their distance from the start node, so that as soon as we visit a node, we immediately know the correct distance to this node. This is guaranteed to terminate after considering each edge at most twice (once from each end in an undirected graph), since we do not expand from nodes that have already been visited. It follows that the running time is 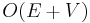 . BFS also solves the problem when some edges are allowed to have weight zero (by using a deque in place of the queue).
. BFS also solves the problem when some edges are allowed to have weight zero (by using a deque in place of the queue).
In a weighted graph with nonnegative weights, it is still possible to visit the vertices in increasing order of distance from the source. This is because the source is obviously the closest to itself, the next closest vertex is obviously one of its immediate neighbors, the next closest is obviously either another immediate neighbor of the source or an immediate neighbor of the second closest vertex, and so on --- the length of a path cannot decrease as more nodes are added to the end of it. So by replacing the queue with a priority queue and greedily picking the next vertex to visit, we obtain Dijkstra's algorithm, which is slower by only a log factor due to the priority queue, 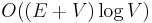 overall in a finite graph. (In a dense graph, it is also possible to implement this in
overall in a finite graph. (In a dense graph, it is also possible to implement this in 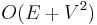 time, which is asymptotically optimal in this case.)
time, which is asymptotically optimal in this case.)
If, on the other hand, edges of negative weight exist, but not in a way that introduces negative-weight cycles, there is still a simple way to find shortest paths, known as the Bellman–Ford algorithm. This works by repeatedly trying to relax each edge in the graph; it is not too hard to show that after doing this enough times, the correct shortest paths will all be known. Specifically, 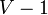 iterations are required, so the running time is
iterations are required, so the running time is 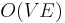 . Another solution, which is sometimes faster, is the Shortest Path Faster Algorithm (SPFA).
. Another solution, which is sometimes faster, is the Shortest Path Faster Algorithm (SPFA).
All-pairs shortest paths[edit]
We might try to find all-pairs shortest paths by running a single-source shortest paths algorithm using each vertex in turn as the source. Hence, we have the following bounds with a binary heap implementation of the priority queue ADT:
-
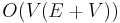 when the graph is unweighted
when the graph is unweighted -
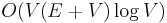 when the edge weights are nonnegative and the graph is sparse (
when the edge weights are nonnegative and the graph is sparse (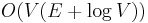 using a Fibonacci heap)
using a Fibonacci heap) -
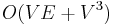 when the edge weights are nonnegative and the graph is dense
when the edge weights are nonnegative and the graph is dense -
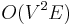 when edge weights are allowed to be negative, but no negative-weight cycles exist.
when edge weights are allowed to be negative, but no negative-weight cycles exist.
There is also a general-purpose technique called the Floyd–Warshall algorithm, which is often considered dynamic, that solves all four cases in 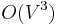 time. It works by using each vertex in turn and using it to try to relax the distance between every pair of nodes in the graph. When the graph is dense, Floyd–Warshall is just as fast as BFS or Dijkstra's, and it always outperforms Bellman–Ford. So we have the bound
time. It works by using each vertex in turn and using it to try to relax the distance between every pair of nodes in the graph. When the graph is dense, Floyd–Warshall is just as fast as BFS or Dijkstra's, and it always outperforms Bellman–Ford. So we have the bound 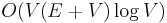 for sparse graphs with nonnegative edge weights and
for sparse graphs with nonnegative edge weights and 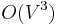 for dense graphs.
for dense graphs.
What if the graph is sparse and it has negative edge weights? Can we do better than 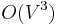 here? Not using the Bellman–Ford algorithm
here? Not using the Bellman–Ford algorithm  times, certainly. However, it turns out that it is possible to run Bellman–Ford once and thus transform the graph into a form in which all edge weights are nonnegative, then run Dijkstra's
times, certainly. However, it turns out that it is possible to run Bellman–Ford once and thus transform the graph into a form in which all edge weights are nonnegative, then run Dijkstra's  times. This gives a method known as Johnson's algorithm that matches the time bound for graphs with nonnegative edge weights (since the time taken to run Bellman–Ford is asymptotically dominated by the time taken to run
times. This gives a method known as Johnson's algorithm that matches the time bound for graphs with nonnegative edge weights (since the time taken to run Bellman–Ford is asymptotically dominated by the time taken to run  invocations of Dijkstra's).
invocations of Dijkstra's).
Single-pair shortest path[edit]
We can compute a single-pair shortest path by taking the source  and running single-source shortest paths from it, and simply extracting the shortest path to the destination
and running single-source shortest paths from it, and simply extracting the shortest path to the destination  . This computes a lot of extra information (namely, the shortest paths to all the other vertices as well), so we might wonder whether it is possible to do better. It turns out that there are no known single-pair shortest path algorithms that outperform single-source shortest paths algorithms in the worst case. Nevertheless, it is often possible to do better in the average case.
. This computes a lot of extra information (namely, the shortest paths to all the other vertices as well), so we might wonder whether it is possible to do better. It turns out that there are no known single-pair shortest path algorithms that outperform single-source shortest paths algorithms in the worst case. Nevertheless, it is often possible to do better in the average case.
(Note: if edges of negative weight are allowed to exist in an infinite graph, then the problem is impossible; if any bound on the running time to find a shortest path is claimed, we can defeat this claim by constructing a graph in which the shortest path involves a highly negatively weighted edge that is extremely far away, too far to be explored within the time bound.)
A* or heuristic search[edit]
In the single-pair shortest path problem, we know exactly where we want to go, we just don't know how to get there. But what if we were able to guess roughly how far away we are from the destination? Then we could proceed as in Dijkstra's algorithm, but give priority to exploring edges that we think take us closer to the destination rather than further away. Formally, we define a heuristic function 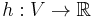 such that
such that 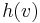 is a "guess" for the actual distance between
is a "guess" for the actual distance between  and
and  (the destination). If we can find such a heuristic function that never overestimates (only underestimates) the correct distance, we can use the A* search algorithm to take advantage of this information to help find a shortest path more quickly. (If
(the destination). If we can find such a heuristic function that never overestimates (only underestimates) the correct distance, we can use the A* search algorithm to take advantage of this information to help find a shortest path more quickly. (If 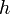 overestimates, then we may still get a relatively short path, but we are not guaranteed that it is a correct shortest path.) The better our estimates with
overestimates, then we may still get a relatively short path, but we are not guaranteed that it is a correct shortest path.) The better our estimates with 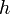 , the faster the search, but in the worst case, in which our heuristic is totally off, we cannot improve much over Dijkstra's.
, the faster the search, but in the worst case, in which our heuristic is totally off, we cannot improve much over Dijkstra's.
Meet-in-the-middle[edit]
Another example of when we don't have to worry much about the worst case, and hence might be able to get a better search time, is when the graph we are searching is extremely large but yet we know that the shortest path is relatively short. For example, consider the Rubik's cube graph, in which each legal position is a vertex and an edge exists between two vertices if the positions they represent can be interconverted with one face turn. There are approximately 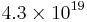 positions of the Rubik's cube, but the shortest path between any pair of vertices always has length 20 or less.[1] The graph we are searching may even be infinite.
positions of the Rubik's cube, but the shortest path between any pair of vertices always has length 20 or less.[1] The graph we are searching may even be infinite.
Meet-in-the-middle search works similarly to a single-source search such as BFS or Djikstra's algorithm, but it differs in that the algorithm branches outward from both the source and the destination (backward along directed edges, if any). In this way we simultaneously build the beginning of the path (by searching from the source) and the end (by searching from the destination). When a common vertex is reached, these two pieces of the path may be assembled to form the full path. To understand why this is faster, imagine we were to execute BFS on the Rubik's Cube graph in order to try to find a path from a scrambled position to the solved position. Each vertex in the graph has degree 18 (three possible moves per face), so, if the distance from the scrambled position to the solved position is, say, 8, we will visit on the order of 188 vertices in the search (about 11 billion). If on the other hand we found this path by finding a path of length 4 from the source and a path of length 4 from the destination that happened to share an endpoint, we would only visit on the order of 2×184 vertices, which is about 210000. So we have cut down the size of the part of the graph we have to explore by a factor of about 50000. Note however that there is no free lunch; we need some way of determining when a vertex has been visited both forward and backward, such as a hash table.
References[edit]
- ↑ Tomas Rokicki et al. "God's Number is 20". Retrieved 2011-03-02 from http://cube20.org/