Johnson's algorithm
Johnson's algorithm is a technique for finding all-pairs shortest paths in a graph in which some edge weights may be negative (but there are no cycles of negative weight). It works by executing the Bellman–Ford algorithm once, using the data obtained to "reweight" the graph, eliminating negative weights, and then running Dijkstra's algorithm  times. Accordingly, its runtime is
times. Accordingly, its runtime is 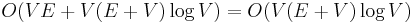 using a binary heap, or
using a binary heap, or 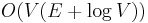 using a Fibonacci heap. Because of this, it is faster to use the Floyd–Warshall algorithm when the graph is dense, but Johnson's algorithm is faster when the graph is sparse.
using a Fibonacci heap. Because of this, it is faster to use the Floyd–Warshall algorithm when the graph is dense, but Johnson's algorithm is faster when the graph is sparse.
Reweighting by vertex
We want to change the weights of edges in the graph so that we can eliminate negative-weight edges, but we have to do so in such a way that the shortest paths do not change at all, otherwise the algorithm will simply not work. We shall do this by reweighting the graph in such a way that, given two vertices  and
and  , the weight of a path after the reweighting is always equal to the weight of the path before the reweighting, plus some constant that depends only on
, the weight of a path after the reweighting is always equal to the weight of the path before the reweighting, plus some constant that depends only on  and
and  but not the path.
but not the path.
A straightforward way of doing this is reweighting by vertex. We shall initially assign each vertex 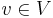 a height
a height 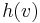 . After we have done this, we will change the weight of any edge
. After we have done this, we will change the weight of any edge 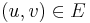 from
from 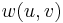 to
to 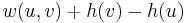 . (Intuitively, think of height literally, i.e., as an altitude, so that whenever we walk along an edge from
. (Intuitively, think of height literally, i.e., as an altitude, so that whenever we walk along an edge from  to
to  , if
, if  is higher, it becomes "harder", i.e., like a higher distance, and if it is lower, it is like a lower distance.)
is higher, it becomes "harder", i.e., like a higher distance, and if it is lower, it is like a lower distance.)
What happens to a path from  to
to  ? Suppose the path is given by
? Suppose the path is given by 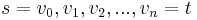 . Then the original weight of this path is
. Then the original weight of this path is 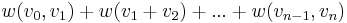 . After reweighting, the weight of this path becomes :
. After reweighting, the weight of this path becomes :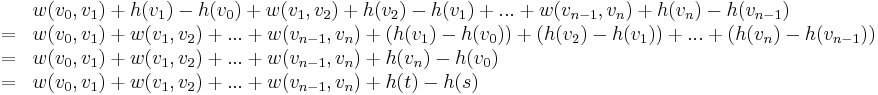
So every path from  to
to  has a new weight equal to its original weight plus the difference in heights between the source and destination, which means a shortest path before the reweighting is still a shortest path after the reweighting, as promised. (With a bit of imagination, this still makes sense intuitively. Imagine the initially flat terrain is subject to geological activity that causes it to become uneven. If the source and the destination are still at the same height, for example, it doesn't matter what happened to the heights along the shortest path --- the amount of uphill has to equal the amount of downhill, crudely speaking, since you end up at the same height at the end. It's just not immediately obvious because even though uphill is harder for us, downhill is not really easier.)
has a new weight equal to its original weight plus the difference in heights between the source and destination, which means a shortest path before the reweighting is still a shortest path after the reweighting, as promised. (With a bit of imagination, this still makes sense intuitively. Imagine the initially flat terrain is subject to geological activity that causes it to become uneven. If the source and the destination are still at the same height, for example, it doesn't matter what happened to the heights along the shortest path --- the amount of uphill has to equal the amount of downhill, crudely speaking, since you end up at the same height at the end. It's just not immediately obvious because even though uphill is harder for us, downhill is not really easier.)
Eliminating negative-weight edges
First, notice that reweighting by vertex cannot eliminate negative-weight cycles. This is because a cycle's weight will not change under reweighting, as a cycle can be considered a path from a vertex to itself (no height difference). However, it is always possible to make all edges non-negative provided that there are no negative-weight cycles.
To do so, we shall make use of the following Lemma:
Lemma: Given three nodes 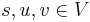 , where a path exists from
, where a path exists from  to
to  and
and  and an edge exists from
and an edge exists from  to
to  , the weight
, the weight 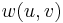 is at least
is at least  . (Here,
. (Here, 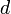 represents the distance function.)
represents the distance function.)
Proof: If 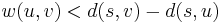 , then
, then 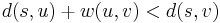 . But this means we can take the shortest path from
. But this means we can take the shortest path from  to
to  and append the edge
and append the edge 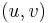 to obtain a path from
to obtain a path from  to
to  with weight less than
with weight less than 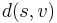 , a contradiction. (This is equivalent to saying that relaxation is still possible.)
, a contradiction. (This is equivalent to saying that relaxation is still possible.) 
Now what happens if we fix a source  and set the height of each vertex
and set the height of each vertex 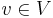 to
to 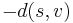 ? Then, the new weight of each edge
? Then, the new weight of each edge 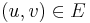 becomes
becomes 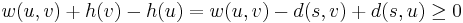 by the Lemma. So we have successfully eliminated all negative weights. All we have to do is find the single-source shortest paths first, which is done using the Bellman–Ford algorithm.
by the Lemma. So we have successfully eliminated all negative weights. All we have to do is find the single-source shortest paths first, which is done using the Bellman–Ford algorithm.
Because the graph may not be connected, it may not be possible to fix a single source 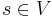 that allows all weights to be calculated at once. To circumvent this problem and allow just one invocation of Bellman–Ford to succeed, we first introduce an extra vertex into the graph, connecting it via edges of weight 0 to all other vertices. (But this vertex must be removed before we proceed to the next step.)
that allows all weights to be calculated at once. To circumvent this problem and allow just one invocation of Bellman–Ford to succeed, we first introduce an extra vertex into the graph, connecting it via edges of weight 0 to all other vertices. (But this vertex must be removed before we proceed to the next step.)
Home stretch
Having reweighted the graph appropriately, we can now run Dijkstra's algorithm once using each vertex as a source.
References
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), Introduction to Algorithms, MIT Press and McGraw-Hill, ISBN 978-0-262-03293-3 . Section 25.3, "Johnson's algorithm for sparse graphs", pp. 636–640.