Map
A map, also known as a dictionary or associative array, is an abstract data type that stores a set of key-value pairs. Hence, a map supports at least the following operations:
- Insert a key into the map, along with a corresponding value, if the key does not already exist in the map (and fail if it does).
- Delete a given key from the map, along with its corresponding value (and fail if the key does not already exist in the map).
- Search for a given key in the map, returning its corresponding value if found.
- Change the value corresponding to a given key in the map.
The following operation is usually supported as well:
- Iterate through the map, obtaining all key-value pairs stored therein.
In statically typed programming languages, the keys must all be of the same type (key type), and the values must also all be of the same type (value type). (However, statically typed languages do often provide a means to achieve varied value types in one map, such as C's void pointers, and Java's generic Object type.) In dynamically typed languages, the values do not necessarily have to be of the same type, but the keys most often are.
The map is a generalized form of the array. Whereas the array requires indices to be consecutive elements of a well-ordered set, a map allows keys of arbitrary type (subject to restrictions imposed by implementation). An important difference, however, is that whereas an array requires memory proportional to the difference between its smallest and largest index, a map usually only requires memory proportional to the amount of data it contains (that is, the total size of the key-value pairs stored therein). There is a trade-off associated with the increased flexibility and lower memory usage, however; operations on maps are invariably slower than operations on arrays, because nontrivial algorithms are required to maintain the map's internal representation in memory.
An ordered map is a kind of map that requires its key type to be totally ordered. Hence, for example, an ordered map can have real numbers or strings as its keys (whereas an array cannot). An ordered map supports all the operations of a map, but its Search operation is more powerful; if the desired key is not found, it can find the least key in the map that is greater than the key given, and iterating through the map is guaranteed to give all of its keys in order.
Contents
Explanation of naming
The name map is fairly easy to understand; a map simply maps a key onto a value. Indeed, we may think of a map as a mutable function given by the set of key-value pairs contained therein (where the set of keys is the domain, the value type is the codomain, and the set of values is the range).
The name associative array reflects the notion that maps are generalized arrays that associate keys with values, whereas ordinary arrays are just passive chunks of memory in which values are found at certain locations and the indices are merely offsets (in C-based languages, in which indices are natural numbers starting from zero) or syntactic sugar for offsets (as in Pascal).
The name dictionary is formed in analogy with actual dictionaries, which map a string (a word) onto another string (a definition).
Implementation
Association list
An association list is simply an unordered list of key-value pairs; this may be implemented as either a linked list or an extensible array without affecting the complexity. The association list originated in Lisp, in which the list is the fundamental data structure (the pairs are also represented as lists). Here, Search, Delete, and Change have a worst-case time complexity linear in the size of the list, as they may have to examine all of its elements, whereas Insert always has to examine all the elements in the list, in case the given key already exists:
| Worst case | Average case | Best case | |
|---|---|---|---|
| Insert | 
|

|

|
| Delete | 
|

|
 (using linked list) (using linked list)
|
| Search | 
|

|

|
| Change | 
|

|

|
| Iterate | 
|

|

|
Hash table
A map implemented using a hash table is also known as a hash map. Hash maps are necessarily unordered, and any key type is permissible as long as a hash function can be defined for it. Strong, general-purpose binary hashes such as SHA1 make it possible to define hash functions on essentially any transparent data type, but in practice custom hashes may be faster to compute, which is significant because every map operation requires computing the hash of the key.
The efficiency and flexibility of hash maps makes them popular and they are often implemented in a programming language's standard library.
| Worst case | Average case | Best case | |
|---|---|---|---|
| Insert | 
|

|

|
| Delete | 
|

|

|
| Search | 
|

|

|
| Change | 
|

|

|
| Iterate | 
|

|

|
A disadvantage of hash tables is that they may occupy a large amount of memory even when they do not contain very many elements.
Self-balancing binary search tree
The usual data structure of choice for implementing the ordered map in memory is the red-black tree, which is the fastest type of self-balancing binary search tree (BBST) for most applications; for example, both Microsoft and GNU implement std::map (and std::set) in the standard libraries that ship with their C++ compilers using a red-black tree.
The memory requirement of a self-balancing binary search tree is good—it is only the total size of the data it orders plus a constant times the total number of nodes (number of keys). If the keys or values are large, then almost all the space occupied by a map implemented as a BBST is being used to store key-value pairs.
| Worst case | Average case | Best case | |
|---|---|---|---|
| Insert | 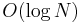
|
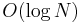
|
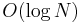
|
| Delete | 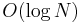
|
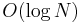
|
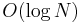
|
| Search | 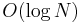
|
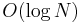
|

|
| Change | 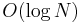
|
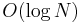
|

|
| Iterate | 
|

|

|
Skip list
Skip lists are not often used in practice, but offer the same time complexity guarantees as BBSTs and are efficient with space as well.
B-tree
When the map is to be stored on disk instead of in primary storage, using a BBST or a skip list will still give 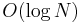 time bounds, but the constant factor may be very high because walking down the tree would require multiple disk reads, each of which has latency in the milliseconds, rather than the nanoseconds it takes to dereference a pointer in RAM. B-trees should be used in this case, as they greatly reduce the number of disk reads while still offering the same asymptotic complexity as BBSTs. (They do not, however, make as efficient use of space.)
time bounds, but the constant factor may be very high because walking down the tree would require multiple disk reads, each of which has latency in the milliseconds, rather than the nanoseconds it takes to dereference a pointer in RAM. B-trees should be used in this case, as they greatly reduce the number of disk reads while still offering the same asymptotic complexity as BBSTs. (They do not, however, make as efficient use of space.)
Trie
If the keys are constrained to be 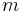 -bit strings (integers between 0 and
-bit strings (integers between 0 and 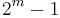 ) then a trie can be used to implement all the ordered map operations in
) then a trie can be used to implement all the ordered map operations in 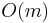 time, that is,
time, that is, 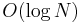 , where
, where 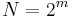 is the maximum size of the map. Asymptotically, this is worse than a BBST implementation if the map will be mostly empty, but it will be faster in most applications. It also tends to use up much more space when it is mostly empty, because of its height, but the discrepancy is smaller when it is mostly full. Conceptually, the trie is much simpler than a BBST, and hence may be preferred in many applications.
is the maximum size of the map. Asymptotically, this is worse than a BBST implementation if the map will be mostly empty, but it will be faster in most applications. It also tends to use up much more space when it is mostly empty, because of its height, but the discrepancy is smaller when it is mostly full. Conceptually, the trie is much simpler than a BBST, and hence may be preferred in many applications.
van Emde Boas tree
Mostly a theoretical curiosity, the van Emde Boas tree is similar to a trie but will do all operations in 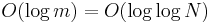 time. However, for reasonable values of
time. However, for reasonable values of  , the speed gains will probably not be worth the extra conceptual complexity. Also, when nearly empty, it may use orders of magnitude more space than the key-value pairs it contains.
, the speed gains will probably not be worth the extra conceptual complexity. Also, when nearly empty, it may use orders of magnitude more space than the key-value pairs it contains.
Iteration
Suppose we wish to double the value associated with a given key in a map, but we don't know what that value is yet. Using the operations given at the beginning of this article, we would need to execute Search to determine the value and then Change to change it to twice what it was before. However, in the typical implementations, this will result in doing more work than necessary. In particular, if a hash table is used, then the hash of the key will be computed twice (once per operation), and it would be nice if we could receive a pointer to the area of memory where the value is stored after executing Search and simply manipulate this instead of starting over with Change. Likewise, it would be nice if we only had to walk down a BBST once rather than twice. For this reason, Search often returns an iterator, an object that represents the location of a key-value pair in the map and may be used to read and modify the value. Assuming the existence of iterators, we can reformulate the operations as follows:
- Insert a new key-value pair into the map, returning an iterator to the newly inserted element (or fail if the given key already exists in the map).
- Delete a given key and its corresponding value from the map, or fail if the given key does not exist in the map.
- Delete the key-value pair referenced by a given iterator from the map.
- Search for a given key in the map, returning an iterator to the key-value pair if found. If the map is ordered, and the key is not found, an iterator to the key-value pair with least key greater than the given key should be returned.
- Begin: Return an iterator to an initial element of the map, or fail if the map is empty. If the map is ordered, this should be the least key.
- Advance: Given an iterator into the map, return an iterator to the "next" element, or fail if the given iterator already refers to the "last" element. If the map is ordered, this should return the iterator to the next key in order (and its corresponding value), or fail if the given iterator already refers to the greatest element in the map. Assuming no intervening insertions or deletions, the sequence of iterators obtained by starting with Begin and repeatedly calling Advance should give all the elements in the map.
In theory, an iterator should remain valid until the key-value pair it refers to is deleted from the map, or the map itself is destroyed. In practice, this is not necessarily so; a std::map::iterator in C++, for example, may become invalidated when other elements are added to or removed from from its map.
Applications
Maps are very useful building blocks of algorithms simply because of their ability to organize data in the same way as arrays. Thus, when objects are identified by, for example, names (strings) rather than by small integers, a map will often be used to store information about these objects that can be quickly looked up by name (which is used as the key in the map). On a larger scale, a relational database with an index is a map, in which the entries in the index column are keys and the rows in which they are found are the corresponding values.
Maps are also used to implement the staircase data structure.
Variations
Multimap
The multimap is a variation on the map that allows a key to be associated with more than one value. The semantics of the operations vary by implementation, and more may be supported than these:
- Insert a new key-value pair into the map. Duplicates are allowed; two or more pairs with the same key and value may be inserted, and all of them are simply stored. This distinguishes the multimap from a set of key-value pairs using the lexicographic ordering (in which the values are required to be comparable as well and duplicates are not allowed.)
- Possibly supported: return an iterator to the newly inserted key-value pair.
- Delete all the key-value pairs with a particular key from the map.
- Possibly supported: delete a specific key-value pair from the map, given by an iterator.
- Search for a specific key in the map, returning all values associated with it, or provide equivalent functionality using iterators.
A simple way to implement a multimap is to use a map in which each key is associated with a linked list of values. Details are left as an exercise to the reader.
Priority queue
The priority queue ADT implements a strict subset of the operations supported by the ordered map, and thus lends itself to faster and simpler implementations.