Lexicographic order
The lexicographic or lexicographical ordering is a technique for constructing an ordering on the set of sequences over the set  from an ordering of
from an ordering of  . A special and often encountered case is that of strings: given an ordering on
. A special and often encountered case is that of strings: given an ordering on 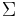 , we can construct an ordering on
, we can construct an ordering on 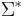 . It is most familiar as the way in which words are ordered in dictionaries: the first character of the first string and the first character of the second string are first compared; if they match then the second character of the first string and the second character of the second string are in turn compared, and so on until either the strings mismatch at the earliest possible position, which decides which string is smaller, or one string runs out of characters, in which the shorter string is smaller. (If they run out at the same time, the strings are equal.) Many programming languages have built-in support for lexicographic comparison of strings and sequences.
. It is most familiar as the way in which words are ordered in dictionaries: the first character of the first string and the first character of the second string are first compared; if they match then the second character of the first string and the second character of the second string are in turn compared, and so on until either the strings mismatch at the earliest possible position, which decides which string is smaller, or one string runs out of characters, in which the shorter string is smaller. (If they run out at the same time, the strings are equal.) Many programming languages have built-in support for lexicographic comparison of strings and sequences.
Examples
The lexicographic ordering inherits the properties of the underlying ordering.
- A partial order on
 will give a partial lexicographic order. For example, the case-insensitive ordering on the Latin alphabet {a, b, ..., z, A, B, ..., Z} allows us to order English words. When a pair of corresponding elements is not comparable, we skip them. The word Poland is smaller than the word polish, for example, because P and p are not comparable, o and o are equal, l and l are equal, but at the fourth position, we have a < i. Likewise, the word polish is smaller than the word polished, because it is a proper prefix, and Polish is also smaller than polished. The words polish and Polish, however, are not comparable, since neither is less than the other, but they are also not equal. (Nevertheless, the term case-insensitive, strictly interpreted, suggests that these strings are to be treated as equal; we have used the term in a slightly different way to demonstrate a partial lexicographic ordering.)
will give a partial lexicographic order. For example, the case-insensitive ordering on the Latin alphabet {a, b, ..., z, A, B, ..., Z} allows us to order English words. When a pair of corresponding elements is not comparable, we skip them. The word Poland is smaller than the word polish, for example, because P and p are not comparable, o and o are equal, l and l are equal, but at the fourth position, we have a < i. Likewise, the word polish is smaller than the word polished, because it is a proper prefix, and Polish is also smaller than polished. The words polish and Polish, however, are not comparable, since neither is less than the other, but they are also not equal. (Nevertheless, the term case-insensitive, strictly interpreted, suggests that these strings are to be treated as equal; we have used the term in a slightly different way to demonstrate a partial lexicographic ordering.) - A total order on
 will give a total lexicographic order. For example, the set {a, b, ..., z} is totally ordered (uppercase letters have been excluded). Because no pair of elements can ever fail to be comparable, no pair of sequences can fail to be comparable, either, under our procedure. Hence again we have poland < polish < polished. (The sequences Poland and Polish are not allowed this time.)
will give a total lexicographic order. For example, the set {a, b, ..., z} is totally ordered (uppercase letters have been excluded). Because no pair of elements can ever fail to be comparable, no pair of sequences can fail to be comparable, either, under our procedure. Hence again we have poland < polish < polished. (The sequences Poland and Polish are not allowed this time.) - A wellorder on
 will give a lexicographic wellorder, which means that, given enough time (potentially infinitely much), we can actually list out all sequences in increasing lexicographic order starting from the empty sequence, which is the smallest. For example, the set {0,1} is well-ordered, and we may well-order the binary strings of length less than or equal to 3 as follows: λ < 0 < 00 < 000 < 001 < 01 < 010 < 011 < 1 < 10 < 100 < 101 < 11 < 110 < 111.
will give a lexicographic wellorder, which means that, given enough time (potentially infinitely much), we can actually list out all sequences in increasing lexicographic order starting from the empty sequence, which is the smallest. For example, the set {0,1} is well-ordered, and we may well-order the binary strings of length less than or equal to 3 as follows: λ < 0 < 00 < 000 < 001 < 01 < 010 < 011 < 1 < 10 < 100 < 101 < 11 < 110 < 111.
Implementation
input strings s, t
fail ← false
for each i ∈ [1..min(length(s),length(t))]
if s[i] < t[i]
done; s is smaller
else if s[i] > t[i]
done; t is smaller
else if s[i] ≠ t[i]
fail ← true
if length(s) < length(t)
done; s is smaller
else if length(s) > length(t)
done; t is smaller
else if fail
done; s and t are not comparable
else
done; s and t are equal