Longest palindromic substring
The longest palindromic substring problem is exactly as it sounds: the problem of finding a maximal-length substring of a given string that is also a palindrome. For example, the longest palindromic substring of bananas is anana. The longest palindromic substring is not guaranteed to be unique; for example, in the string abracadabra, there is no palindromic substring with length greater than three, but there are two palindromic substrings with length three, namely, aca and ada. In some applications it may be necessary to return all maximal-length palindromic substrings, in some, only one, and in some, only the maximum length itself. This article discusses algorithms for solving these problems.
Contents
Theoretical discussion
Lower bound
The worst-case running time of any correct algorithm must be at least 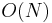 , where
, where  is the length of the string. This is because the algorithm cannot be correct unless it can verify whether the entire string is a palindrome (because in that case it is itself the longest palindromic substring), and it is not possible to conclude that a string is palindromic unless every character is examined.
is the length of the string. This is because the algorithm cannot be correct unless it can verify whether the entire string is a palindrome (because in that case it is itself the longest palindromic substring), and it is not possible to conclude that a string is palindromic unless every character is examined.
One might ask whether the size of the output gives a better lower bound on the worst-case running time in the case in which it is necessary to return all maximal-length palindromic substrings (rather than simply reporting the maximum length). It turns out that it does not, because there can only be up to linearly many substrings of any given length. Specifically, there cannot be more than  different palindromic substrings of maximal length, because there cannot be more than
different palindromic substrings of maximal length, because there cannot be more than  substrings of any given length in the first place.
substrings of any given length in the first place.
Upper bound
Given a substring of length  , we can determine whether it is a palindrome in
, we can determine whether it is a palindrome in 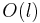 time by iterating through it and checking whether the character at zero-based offset
time by iterating through it and checking whether the character at zero-based offset 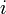 always matches that at
always matches that at 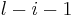 . Furthermore, our original string, of length
. Furthermore, our original string, of length  , has
, has 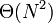 substrings each of length
substrings each of length 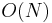 . Therefore, we conclude, by enumerating all substrings of our original string, checking whether each is a palindrome, and finding the longest one which is, we obtain an
. Therefore, we conclude, by enumerating all substrings of our original string, checking whether each is a palindrome, and finding the longest one which is, we obtain an 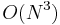 solution. Thus
solution. Thus 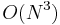 is an upper bound on the efficiency of the best algorithm, and we have established that the longest palindromic substring problem can be solved in polynomial time.
is an upper bound on the efficiency of the best algorithm, and we have established that the longest palindromic substring problem can be solved in polynomial time.
Observation
Every palindromic substring has a centre. For an odd-length substring, this is its middle character; for an even-length substring, this is the imaginary space between its two middle characters. Call each character and each space in the original string a position. Then there are 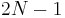 positions in any string of length
positions in any string of length  , and any longest palindromic substring must have one of these as its centre.
, and any longest palindromic substring must have one of these as its centre.
Therefore, if we iterate through all positions of the string, and for each one determine the longest palindromic substring centered on that position, then one of these is the longest palindromic substring of the whole string. For example, in the string opposes, the longest palindromic substrings centered around each position are [o, (empty), p, oppo, p, (empty), o, (empty), s, (empty), ses, (empty), s], and one of these --- oppo --- is the longest palindromic substring of the original string.
Being a bit clever in determining the longest palindromic substring centered about a given string improves the running time over the naive solution dramatically. We begin by noting that there definitely is a palindromic substring of length zero (the empty string) centered around the current center, if it is a space, or a palindromic substring of length one (the character itself) centered around the current center, if it is a character. Then, we repeatedly attempt to make a longer palindromic substring centered at our current location by adding the characters just before and just after the current longest palindromic substring. We can do this if and only if these characters match. If they do not match, there is no hope of any longer palindromic substring centered here existing, so we are done.
For example, suppose our current center is between the two b's in the word scabbards. We already know there exists a palindromic substring of length zero (the empty string) centered around our current location. To determine whether we can make it longer, we check the first character on either side, that is, the two b's. They match, so we know that bb is a palindromic substring centered at our current location. Then we try to extend it again, by checking the first character on either side. Now we find two a's, so we now know we have abba, a palindromic substring of length 4, centered around our current location. Again we try to extend it, by checking one character on each side. We find the c and the r, which do not match. Therefore we know that abba is the longest palindromic substring centered our current location --- substrings centered at our current location that are longer than cabbar, such as scabbard, have no hope of being palindromic.
Notice that once we have fixed the centre, we will not examine any character of the string more than once in determining the longest palindromic substring centered there. That is, determining the longest palindromic substring centered at any given location takes only 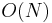 time, and by iterating over all possible centres, an
time, and by iterating over all possible centres, an 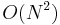 algorithm is obtained.
algorithm is obtained.
Toward a better bound
Thus, the best possible worst-case running time lies between 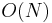 and
and 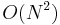 . We now show that the problem can be solved in
. We now show that the problem can be solved in 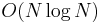 time using standard data structures from the literature, the suffix tree and the suffix array.
time using standard data structures from the literature, the suffix tree and the suffix array.
Suffix array
The suffix array is a sorted list of the suffixes of a given string, indexed by first character. For example, the suffix array of bananas is [1, 3, 5, 0, 2, 4, 6], corresponding to the suffixes [ananas, anas, as, bananas, nanas, nas, s]. Simple linear-time algorithms now exist for computation of suffix arrays of strings with constant or integer alphabets.[1]
Once the suffix array of a string has been computed, a simple linear-time algorithm[2] will compute the length of the longest common prefix of each pair of adjacent suffixes in the suffix array. The array containing these lengths is known as the lcp array.
If we want to know the longest common prefix of any pair of suffixes, not necessarily lexicographically adjacent, we locate those two suffixes in the suffix array and then find the minimum entry in the lcp array in the range they delimit, hence reducing the problem to a range minimum query. For example, the string teetertotter has suffix array [1,10,4,2,7,11,5,0,9,3,6,8] and lcp array [1,2,1,0,0,1,0,2,3,1,1], because the suffixes starting at positions 1 and 10 have one character in common at the beginning, the suffixes starting at positions 10 and 4 have two characters in common at the beginning, and so on. Suppowe we want to determine the length of the longest common prefix of the suffixes totter (6) and tter (8), which are not adjacent in the suffix array. We locate 6 and 8 in the suffix array, and we see from the lcp array that the longest common prefixes of the pairs of suffixes starting at locations 9 and 3, 3 and 6, and 6 and 8 have lengths 3, 1, and 1, respectively. This is a contiguous range of the lcp array. The minimum value in this array, 1, is the answer.
To solve the problem at hand, we will concatenate our string with a unique separator and a reversed copy of itself, so that rearrangement becomes, for example, rearrangement#tnemegnarraer, and then build the suffix array and longest common prefix array for the new string. Then we iterate through all positions in the original string and find the longest palindromic substring centered at each one. To do so, we mirror the current position across the centre of the string, and then take longest common prefixes.
Even case
To determine the longest palindromic substring centered between the two r's (which must be of even length), we consider the suffixes starting at the underlined locations: rearrangement#tnemegnarraer. We see that the longest common prefix of these two suffixes has length 2 (underlined: rearrangement#tnemegnarraer). But because the second half is a reversed copy of the first half, we know the ra in the second half is actually the ar in the first half just before our current position: rearrangement#tnemegnarraer. Thus we have determined that the longest palindromic substring here has length 4. In general we find the character just after our current position in the original string, and the character just before it in the reversed string, and find the longest common prefix using the lcp array and RMQ.
Odd case
In the odd case, we are centered at some character of the original string. In this case, we examine the suffix starting at the character in the original string immediately following it, and the suffix in the reversed string starting at the character immediately preceding it. If we were centered at the m in rearrangement, then, we would be examining the suffixes starting at the underlined characters: rearrangement#tnemegnarraer. We see that the longest common prefix has length 1, and we reflect the e in the reversed half back onto its position in the first half, hence, rearrangement#tnemegnarraer is the longest palindromic substring centered at the m.
Complexity
Since 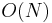 positions for the centre are considered, and a range minimum query can be executed in
positions for the centre are considered, and a range minimum query can be executed in 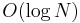 time (or constant time with
time (or constant time with 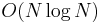 preprocessing), the time complexity of this solution is
preprocessing), the time complexity of this solution is 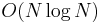 .
.
Suffix tree
The suffix tree is a compressed trie of the suffixes of the string. A detailed discussion of the structure of the suffix tree is given in the article. There exist linear-time algorithms[3] for construction of suffix trees, as well. There are two possible approaches here: we can either concatenate the string with a unique separator and a reversed copy of itself, as with the suffix array, or we can build a generalized suffix tree of the string and its reverse. We proceed as we did with the even and odd cases in the suffix array section, finding longest common prefixes starting at almost-corresponding positions in the original and reverse strings. It is not too hard to see that this is a lowest common ancestor query on the tree. For example, to find the longest palindromic substring of even length centered between the two r's in rearrangement, we could build the suffix tree for rearrangement#tnemegnarraer, locate the leaves corresponding to the suffixes starting at the underlined characters, and find their lowest common ancestor. The depth of this node is the length of the longest common prefix of these two suffixes. Here it is 2, so we know that the substrings underlined match: rearrangement#tnemegnarraer, giving the palindromic substring rearrangement#tnemegnarraer. LCA queries can be executed in constant time after 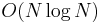 preprocessing time, giving an
preprocessing time, giving an 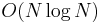 solution.
solution.
Existence of a linear-time algorithm
It is possible to execute 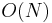 LCA queries on a tree with
LCA queries on a tree with 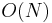 nodes in
nodes in 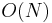 time using a technique due to Gabow and Tarjan.[4] This shows that a linear-time solution exists, which puts to rest the question of the best possible efficiency for a solution to the longest palindromic substring problem.
time using a technique due to Gabow and Tarjan.[4] This shows that a linear-time solution exists, which puts to rest the question of the best possible efficiency for a solution to the longest palindromic substring problem.
References
- ↑ Juha Kärkkäinen and Peter Sanders. 2003. Simple linear work suffix array construction. In Proceedings of the 30th international conference on Automata, languages and programming (ICALP'03), Jos C. M. Baeten, Jan Karel Lenstra, Joachim Parrow, and Gerhard J. Woeginger (Eds.). Springer-Verlag, Berlin, Heidelberg, 943-955. Retrieved 2010-11-13 from http://monod.uwaterloo.ca/~cs482/suffix-icalp03.pdf.
- ↑ Toru Kasai, Gunho Lee, Hiroki Arimura, Setsuo Arikawa, and Kunsoo Park. 2001. Linear-Time Longest-Common-Prefix Computation in Suffix Arrays and Its Applications. In Proceedings of the 12th Annual Symposium on Combinatorial Pattern Matching (CPM '01), Amihood Amir and Gad M. Landau (Eds.). Springer-Verlag, London, UK, 181-192.
- ↑ E. Ukkonen. (1995). On-line construction of suffix trees. Algorithmica 14(3):249-260. PDF | PDF with figures
- ↑ Gabow, H. N.; Tarjan, R. E. (1983), "A linear-time algorithm for a special case of disjoint set union", Proceedings of the 15th ACM Symposium on Theory of Computing (STOC), pp. 246–251, doi:10.1145/800061.808753