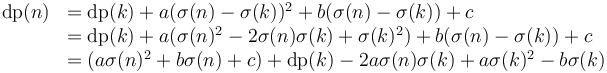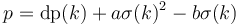Convex hull trick
The convex hull trick is a technique (perhaps best classified as a data structure) used to determine efficiently, after preprocessing, which member of a set of linear functions in one variable attains an extremal value for a given value of the independent variable. It has little to do with convex hull algorithms.
Contents
History
The convex hull trick is perhaps best known in algorithm competitions from being required to obtain full marks in several USACO problems, such as MAR08 "acquire", which began to be featured in national olympiads after its debut in the IOI '02 task Batch Scheduling, which itself credits the technique to a 1995 paper (see references). Very few online sources mention it, and almost none describe it. It has been suggested (van den Hooff, 2010) that this is because the technique is "obvious" to anybody who has learned the sweep line algorithm for the line segment intersection problem.
The problem
Suppose that a large set of linear functions in the form 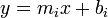 is given along with a large number of queries. Each query consists of a value of
is given along with a large number of queries. Each query consists of a value of  and asks for the minimum value of
and asks for the minimum value of  that can be obtained if we select one of the linear functions and evaluate it at
that can be obtained if we select one of the linear functions and evaluate it at  . For example, suppose our functions are
. For example, suppose our functions are 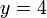 ,
, 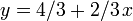 ,
, 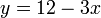 , and
, and 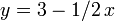 and we receive the query
and we receive the query 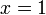 . We have to identify which of these functions assumes the lowest
. We have to identify which of these functions assumes the lowest  -value for
-value for 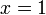 , or what that value is. (It is the function
, or what that value is. (It is the function 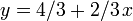 , assuming a value of 2.)
, assuming a value of 2.)
The variation in which we seek the maximal line, not the minimal one, is a trivial modification and we will focus our attention on finding the minimal line.
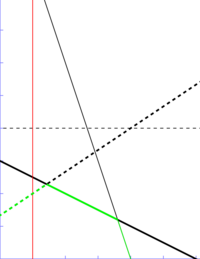
When the lines are graphed, this is easy to see: we want to determine, at the -coordinate 1 (shown by the red vertical line), which line is "lowest" ( has the lowest
-coordinate 1 (shown by the red vertical line), which line is "lowest" ( has the lowest  -coordinate). Here it is the heavy dashed line,
-coordinate). Here it is the heavy dashed line, 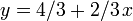 .
.
Naive algorithm
For each of the 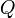 queries, of course, we may simply evaluate every one of the linear functions, and determine which one has the least value for the given
queries, of course, we may simply evaluate every one of the linear functions, and determine which one has the least value for the given  -value. If
-value. If 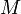 lines are given along with
lines are given along with 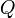 queries, the complexity of this solution is
queries, the complexity of this solution is 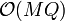 . The "trick" enables us to speed up the time for this computation to
. The "trick" enables us to speed up the time for this computation to 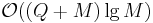 , a significant improvement.
, a significant improvement.
Another example: APIO 2010 Commando
You are given:
- A sequence of
 positive integers (
positive integers (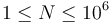 ).
). - The integer coefficients of a quadratic function
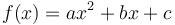 , where
, where 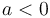 .
.
The objective is to partition the sequence into contiguous subsequences such that the sum of  taken over all subsequences is maximized, where the value of a subsequence is the sum of its elements.
taken over all subsequences is maximized, where the value of a subsequence is the sum of its elements.
An 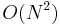 dynamic programming approach is not hard to see.
We define:
dynamic programming approach is not hard to see.
We define:
-
sum(i,j) = x[i] + x[i+1] + ... + x[j] -
adjust(i,j) = a*sum(i,j)^2 + b*sum(i,j) + c
Then let
![\operatorname{dp}(n) = \max_{0 \le k < n} [\operatorname{dp}(k) + \operatorname{adjust}(k+1, n)]](/wiki/images/math/f/a/b/fabeae523532530f49929716692c436f.png) .
.
Pseudocode:
dp[0] ← 0
for n ∈ [1..N]
for k ∈ [0..n-1]
dp[n] ← max(dp[n], dp[k] + adjust(k + 1 , n))
Now let's play around with the function "adjust".
Denote 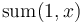 by
by 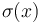 . Then, for some value of
. Then, for some value of  , we can write
, we can write
Now, let
Then, we see that 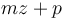 is the quantity we aim to maximize by our choice of
is the quantity we aim to maximize by our choice of  . Adding
. Adding 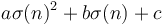 (which is independent of
(which is independent of  ) to the maximum gives the correct value of
) to the maximum gives the correct value of 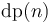 . Also,
. Also, 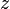 is independent of
is independent of  , whereas
, whereas 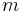 and
and 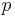 are independent of
are independent of  , as required.
, as required.
Unlike in task "acquire", we are interested in building the "upper envelope". We notice that the slope of the "maximal" line increases as  increases. Since the problem statement indicates
increases. Since the problem statement indicates 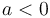 , the slope of each line is positive.
, the slope of each line is positive.
Suppose 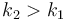 . For
. For 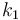 we have slope
we have slope 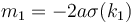 . For
. For 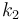 we have slope
we have slope 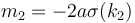 . But
. But 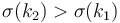 ,
and since the given sequence is positive, so
,
and since the given sequence is positive, so 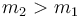 . We conclude that lines are added to our data structure in increasing order of slope.
. We conclude that lines are added to our data structure in increasing order of slope.
Since 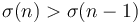 , query values are given in increasing order and a pointer walk suffices (it is not necessary to use binary search.)
, query values are given in increasing order and a pointer walk suffices (it is not necessary to use binary search.)
Fully dynamic variant
The convex hull trick is easy to implement when all insertions are given before all queries (offline version) or when each new line inserted has a lower slope than any line currently in the envelope. Indeed, by using a deque, we can easily allow insertion of lines with higher slope than any other line as well. However, in some applications, we might have no guarantee of either condition holding. That is, each new line to be added may have any slope whatsoever, and the insertions may be interspersed with queries, so that sorting the lines by slope ahead of time is impossible, and scanning through an array to find the lines to be removed could take linear time per insertion
It turns out, however, that it is possible to support arbitrary insertions in amortized logarithmic time. To do this, we store the lines in an ordered dynamic set (such as C++'s std::set). Each line possesses the attributes of slope and y-intercept, the former being the key, as well as an extra 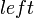 field, the minimum
field, the minimum  -coordinate at which this line is the lowest in the set. To insert a new line, we merely insert it into its correct position in the set, and then all the lines to be removed, if any, are contiguous with it. The procedure is then largely the same as for the case in which we always inserted lines of minimal slope: if the line to be added is
-coordinate at which this line is the lowest in the set. To insert a new line, we merely insert it into its correct position in the set, and then all the lines to be removed, if any, are contiguous with it. The procedure is then largely the same as for the case in which we always inserted lines of minimal slope: if the line to be added is 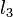 , the line to the left is
, the line to the left is 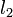 , and the line to the left of that is
, and the line to the left of that is 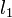 , then we check if the
, then we check if the 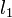 -
-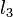 intersection is to the left of the
intersection is to the left of the 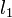 -
-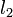 intersection; if so,
intersection; if so, 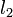 is discarded and we repeat; similarly, if lines
is discarded and we repeat; similarly, if lines 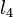 and
and 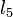 are on the right, then
are on the right, then 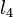 can be removed if the
can be removed if the 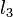 -
-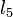 intersection is to the left of the
intersection is to the left of the 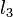 -
-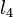 intersection, and this too is performed repeatedly until no more lines are to be discarded. We compute the new
intersection, and this too is performed repeatedly until no more lines are to be discarded. We compute the new 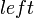 values (for
values (for 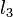 , it is the
, it is the 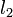 -
-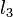 intersection, and for
intersection, and for 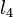 , it is the
, it is the 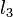 -
-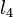 intersection).
intersection).
To handle queries, we keep another set, storing the same data but this time ordered by the 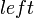 value. When we insert or remove lines from that set (or update, in the case of
value. When we insert or remove lines from that set (or update, in the case of 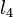 above), we use the
above), we use the 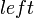 value from the element in that set to associate it with an element in this one. Whenever a query is made, therefore, all we have to do is to find the greatest
value from the element in that set to associate it with an element in this one. Whenever a query is made, therefore, all we have to do is to find the greatest 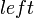 value in this set that is less than the query value; the corresponding line is the optimal one .
value in this set that is less than the query value; the corresponding line is the optimal one .
References
- Brucker, P. (1995). Efficient algorithms for some path partitioning problems. Discrete Applied Mathematics, 62(1-3), 77-85.
- Christiano, Paul. (2007). Land acquisition. Retrieved from an archived copy of the competition problem set at http://tjsct.wikidot.com/usaco-mar08-gold
- Peng, Richard. (2008). USACO MAR08 problem 'acquire' analysis. Retrieved from http://ace.delos.com/TESTDATA/MAR08.acquire.htm
- van den Hooff, Jelle. (2010). Personal communication.
- Wang, Hanson. (2010). Personal communication.