Segment tree

The segment tree is a highly versatile data structure, based upon the divide-and-conquer paradigm, which can be thought of as a tree of intervals of an underlying array, constructed so that queries on ranges of the array as well as modifications to the array's elements may be efficiently performed.

Motivation

One of the most common applications of the segment tree is the solution to the range minimum query problem. In this problem, we are given some array and repeatedly asked to find the minimum value within some specified range of indices. For example, if we are given the array [9,2,6,3,1,5,0,7], we might be asked for the minimum element between the third and the sixth, inclusive, which would be 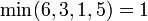$\min(6,3,1,5) = 1$. Then, another query might ask for the minimum element between the first and third, inclusive, and we would answer 2, and so on. Various solutions to this problem are discussed in the range minimum query article, but the segment tree is often the most appropriate choice, especially when modification instructions are interspersed with the queries.

The divide-and-conquer solution

The divide-and-conquer solution would be as follows:

• If the range contains one element, that element itself is trivially the minimum within that range.
• Otherwise, divide the range into two smaller ranges, each approximately half the size of the original, and find their respective minima. The minimum for the original range is then the smaller of the two minima of the sub-ranges.

Hence, if 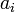$a_i$ denotes the 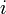$i$^th element in the array, finding the minimum could be encoded as the following recursive function:

$\displaystyle f(x,y) = \begin{cases} a_x & \mathrm{if\ } x = y \\ \min(f(x,\lfloor\frac{x+y}{2}\rfloor),f(\lfloor\frac{x+y}{2}\rfloor+1,y)) & \mathrm{otherwise} \\ \end{cases}$

assuming that 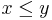$x \le y$.
Hence, for example, the first query from the previous section would be 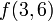$f(3,6)$ and it would be recursively evaluated as $\min(f(3,4),f(5,6))$.

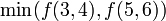Structure

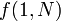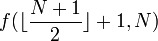Suppose that we use the function defined above to evaluate $f(1,N)$, where $N$ is the number of elements in the array. When $N$ is large, this recursive call has two "children", one of which is the recursive call $f(1,\lfloor\frac{N+1}{2}\rfloor)$, and the other one of which is $f(\lfloor\frac{N+1}{2}\rfloor+1,N)$. Each of these children will then have two children of its own, and so on, down until the base case is reached. If we represent these recursive calls with a tree structure, the call 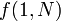$f(1,N)$ would be the root, it would have two children, each child would have two more children, and so on; the base cases would be the leaves of the tree. We are now ready to specify the structure of the segment tree:

• it is a binary tree which represents some underlying array;
• each node is associated with some interval of the array and contains the value(s) of one or more functions of the elements in that interval;
• the root node is associated with the entire array (i.e. the interval $[1,N]$);
• each leaf is associated with an individual element;
• each non-leaf node has two children whose associated intervals are disjoint, and the union of the intervals associated with the two children is the interval associated with the parent;
• each child's interval has approximately half the size of the parent's interval;
• the data stored in each non-leaf node is not only a function of the elements in its associated interval but also a function of the data stored in its children.

That is, the structure of the segment tree is exactly that of the recursive call tree of the function 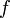$f$ defined above (up to some minor details, such as whether the middle element of an interval of odd size belongs to the left child interval or the right).
Hence, for example, the root node of the array [9,2,6,3,1,5,0,7] would contain the number 0: the minimum of the entire array. Its left child would contain the minimum of [9,2,6,3], that is, 2, and the right would contain the minimum of [1,5,0,7], that is, 0. Evidently, the datum stored in the root node, 0, is the minimum of the data stored at its immediate children, 0 and 2. Similarly, the datum 2 stored in the left child is the minimum of the data stored at its immediate children, 2 and 3 (which are the minima in [9,2] and [6,3], respectively). Each individual element in the array has a leaf node, which merely contains that element itself. (The minimum of a range containing a single element is, of course, the element itself.)