Lowest common ancestor
From PEGWiki
Revision as of 06:57, 9 December 2011 by Brian (Talk | contribs) (Created page with "The '''lowest common ancestor''' or '''least common ancestor''' (LCA) of a nonempty set of nodes in a rooted tree is the unique node of greatest depth that is an ancestor of ...")
The lowest common ancestor or least common ancestor (LCA) of a nonempty set of nodes in a rooted tree is the unique node of greatest depth that is an ancestor of every node in the set. (In biology, this corresponds to the most recent common ancestor of a set of organisms.) We will denote the LCA of a set of nodes 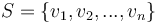 by
by 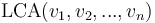 or by
or by 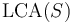 .
.
Properties
The proofs of these properties are left as an exercise to the reader.
-
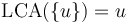 .
. - If
 is an ancestor of
is an ancestor of  , then
, then 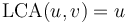 .
. - If neither
 nor
nor  is an ancestor of the other, than
is an ancestor of the other, than  and
and  lie in different subtrees of
lie in different subtrees of 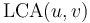 .
. - The entire set of common ancestors of
 is given by
is given by 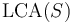 and all of its ancestors (all the way up to the root of the tree).
and all of its ancestors (all the way up to the root of the tree). -
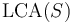 precedes all nodes in
precedes all nodes in  in the tree's preordering, and follows all nodes in
in the tree's preordering, and follows all nodes in  in the tree's postordering.
in the tree's postordering. - If
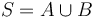 with
with  and
and  both nonempty, then
both nonempty, then 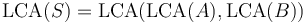 . For example,
. For example, 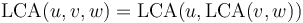 . (The LCA shares this property with the similar-sounding lowest common multiple and greatest common divisor.)
. (The LCA shares this property with the similar-sounding lowest common multiple and greatest common divisor.)